
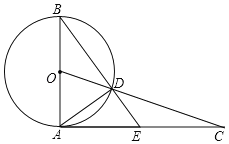
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD,
(1)求证:CD2=CEAC;
(2)若AB=4,AC=4![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)2![]()
【解析】
(1)通过证明△CDE∽△CAD可得结论.
(2)利用相似三角形的性质,勾股定理求出AC,CE即可解决问题.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠B+∠BAD=90°,
∵AC为⊙O的切线,
∴BA⊥AC,
∴∠BAC=90°,即∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∵OB=OD,
∴∠B=∠ODB,
而∠ODB=∠CDE,
∴∠B=∠CDE,
∴∠CAD=∠CDE,
而∠ECD=∠DCA,
∴△CDE∽△CAD;
∴![]() ,
,
∴CD2=CEAC.
(2)解:在Rt△AOC中,∵AB=4,
∴OA=2,AC=4![]() ,
,
∴O=![]() ,
,
∴CD=OC﹣OD=6﹣2=4,
∵CD2=CEAC,
∴CE=2![]() ,
,
∴AE=AC﹣CE=4![]() ﹣2
﹣2![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
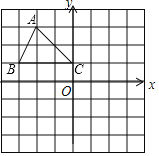
【题目】如图,在平面直角坐标系中,△ABC三个顶点都在格点上,点A,B,C的坐标分别为A(﹣2,3),B(﹣3,1),C(0,1)请解答下列问题:
(1)△ABC与△A1B1C1关于原点O成中心对称,画出△A1B1C1并直接写出点A的对应点A1的坐标;
(2)画出△ABC绕点C顺时针旋转90°后得到的△A2B2C,并求出线段AC旋转时扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
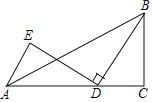
【题目】如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
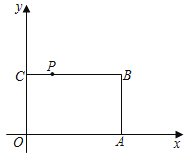
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边O在x轴上,OC在y轴上,OA=6,OC=4,PC=![]() BC.将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转,则第2019秒时,点P的坐标为( )
BC.将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转,则第2019秒时,点P的坐标为( )
A.(3![]() ,
,![]() )B.(2,﹣1)
)B.(2,﹣1)
C.(![]() ,﹣3
,﹣3![]() )D.(﹣1,2)
)D.(﹣1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
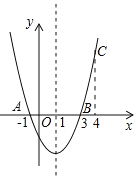
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:
①△AED≌△DFB;②S四边形 BCDG=![]() CG2;③若AF=2DF,则BG=6GF
CG2;③若AF=2DF,则BG=6GF
,其中正确的结论
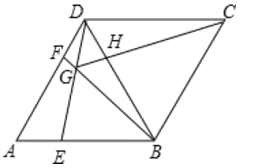
A.只有①②.B.只有①③.C.只有②③.D.①②③.
查看答案和解析>>
科目:初中数学 来源: 题型:
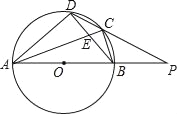
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
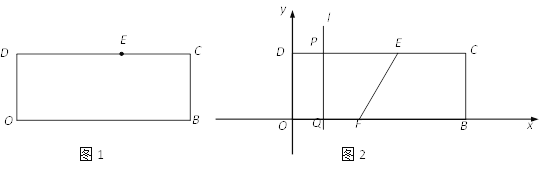
【题目】定义:如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点.如矩形OBCD中,点C为O,B两点的勾股点,已知OD=4,在DC上取点E,DE=8.
(1)如果点E是O,B两点的勾股点(点E不在点C), 试求OB的长;
(2)如果OB=12,分别以OB,OD为坐标轴建立如图2的直角坐标系,在x轴上取点F(5,0).在线段DC上取点P, 过点P的直线l∥y轴,交x轴于点Q.设DP=t.
①当点P在DE之间,以EF为直径的圆与直线l相切,试求t的值;
②当直线l上恰好有2点是E,F两点的勾股点时,试求相应t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
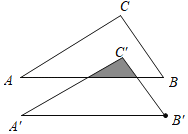
【题目】如图,将Rt△ABC平移到△A'B'C'的位置,其中∠C=90°使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com