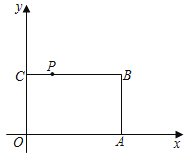
【题目】如图，在平面直角坐标系xOy中，矩形OABC的边O在x轴上，OC在y轴上，OA＝6，OC＝4，PC＝
BC．将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转，则第2019秒时，点P的坐标为（ ）
A.（3
，）B.（2，﹣1）
C.（，﹣3）D.（﹣1，2）
【答案】C
【解析】
将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转，360°÷45°＝8，8秒循环一次，因为2019÷8＝252余数为3，推出第2019秒时，点P旋转到如图P′处，作C′E⊥OC于E，P′F⊥C′E，利用等腰直角三角形的性质即可解决问题．
∵将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转，360°÷45°＝8，
∴8秒循环一次，
∵2019÷8＝252余数为3，
∴第2019秒时，点P旋转到如图P′处，作C′E⊥OC于E，P′F⊥C′E，
由题意△P′C′F，△OEC′都是等腰直角三角形，
∴OE＝C′E＝
×4＝2
，P′F＝C′F＝×2＝，
∴P′（，﹣3），
故选：C．
科目：初中数学 来源： 题型：
【题目】有七张正面标有数字﹣3，﹣2，﹣1，0，1，2，3的卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗均后从中随机抽取一张，记卡片上的数字为a，则使关于x的一元二次方程ax2﹣（2a﹣1）x+a﹣2＝0有两个不相等的实数根，且分式方程
的解为正数的概率为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
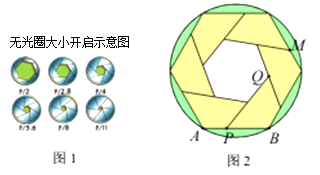
【题目】小明发现相机快门打开过程中，光圈大小变化如图1所示，于是他绘制了如图2所示的图形．图2中留个形状大小都相同的四边形围成一个圆的内接六边形和一个小正六边形，若PQ所在的直线经过点M，PB=5cm，小正六边形的面积为
cm2，则该圆的半径为________cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以矩形ABCD的边CD为直径作⊙O，点E是AB 的中点，连接CE交⊙O于点F，连接AF并延长交BC于点H．
（1）若连接AO，试判断四边形AECO的形状，并说明理由；
（2）求证：AH是⊙O的切线；
（3）若AB＝6，CH＝2，则AH的长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
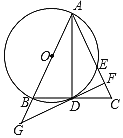
【题目】如图，△ABC中，AB＝AC，以AB为直径的圆O交BC于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G．
（1）求证：DF是⊙O的切线；
（2）已知BD＝
，CF＝2，求DF和BG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】正方形ABCD与正方形DEFG按如图1放置，点A，D，G在同一条直线上，点E在CD边上，AD＝3，DE＝
，连接AE，CG
（1）线段AE与CC的关系为______；
（2）将正方形DEFG绕点D顺时针旋转一个锐角后，如图2，请问（1）中的结论是否仍然成立？请说明理由
（3）在正方形DEFG绕点D顺时针旋转一周的过程中，当∠AEC＝90°时，请直接写出AE的长．
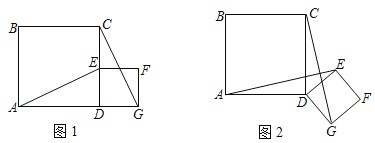
查看答案和解析>>
科目：初中数学 来源： 题型：
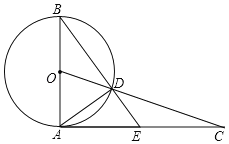
【题目】如图，AB是⊙O的直径，过点A作⊙O的切线并在其上取一点C，连接OC交⊙O于点D，BD的延长线交AC于E，连接AD，
（1）求证：CD2＝CEAC；
（2）若AB＝4，AC＝4
，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
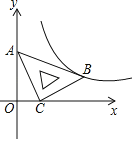
【题目】在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（ ）
A.（
，0）B.（2，0）C.（
，0）D.（3，0）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点C在线段AB上，（点C不与A、B重合），分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE，连接AE、BD交于点P．
（观察猜想）
①AE与BD的数量关系是 ；
②∠APD的度数为 ．
（数学思考）
如图2，当点C在线段AB外时，（1）中的结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明；
（拓展应用）
如图3，点E为四边形ABCD内一点，且满足∠AED＝∠BEC＝90°，AE＝DE，BE＝CE，对角线AC、BD交于点P，AC＝10，则四边形ABCD的面积为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com