
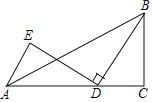
【题目】如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.
【答案】![]()
【解析】
由旋转的性质可知BD=DE,∠C=90°,则容易想到构造一个直角三角形与Rt△BCD全等,即过E点作EH⊥AD于点H,设CD=x,则可用x表示AE的长,从而判断什么时候AE取得最小值.
设CD=x,则AD=5﹣x,
过点E作EH⊥AD于点H,如图:
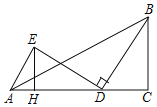
由旋转的性质可知BD=DE,
∵∠ADE+∠BDC=90°,∠BDC+∠CBD=90°,
∴∠ADE=∠CBD,
又∵∠EHD=∠C,
∴△BCD≌△DHE,
∴EH=CD=x,DH=BC=3.
∵AD=5﹣x,
∴AH=AD﹣DH=5﹣x﹣3=2﹣x,
∵在Rt△AEH中,AE2=AH2+EH2=(2﹣x)2+x2=2x2+4x+4=2(x﹣1)2+2,
所以当x=1时,AE2取得最小值2,即AE取得最小值![]() .
.
故答案是:![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点A,沿顺时针方向旋转后得到Rt△AB1C1,当点B1恰好落在斜边BC的中点时,则∠B1AC=( )

A.25°B.30°C.40°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③DP2=PHPC;④FE:BC=![]() ,其中正确的个数为( )
,其中正确的个数为( )
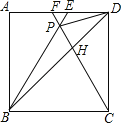
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中留个形状大小都相同的四边形围成一个圆的内接六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为![]() cm2,则该圆的半径为________cm.
cm2,则该圆的半径为________cm.
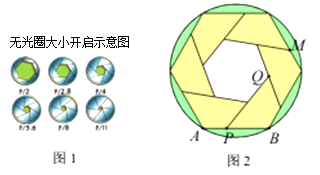
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
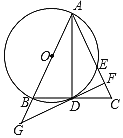
【题目】如图,△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)求证:DF是⊙O的切线;
(2)已知BD=![]() ,CF=2,求DF和BG的长.
,CF=2,求DF和BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
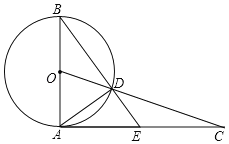
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD,
(1)求证:CD2=CEAC;
(2)若AB=4,AC=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3经过A(3,0),B(1,0)两点(如图1),顶点为M.
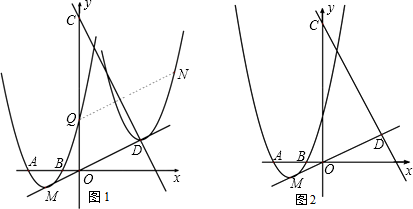
(1)a、b的值;
(2)设抛物线与y轴的交点为Q(如图1),直线y=2x+9与直线OM交于点D. 现将抛物线平移,保持顶点在直线OD上.当抛物线的顶点平移到D点时,Q点移至N点,求抛物线上的两点M、Q间所夹的曲线MQ扫过的区域的面积;
(3)设直线y=2x+9与y轴交于点C,与直线OM交于点D(如图2).现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)没有公共点时,试探求其顶点的横坐标h的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com