
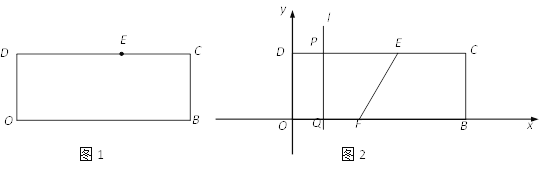
����Ŀ�����壺���һ�����������������㹹��ֱ�������Σ���������Ϊ����������Ĺ��ɵ㣮�����OBCD�У���CΪO��B����Ĺ��ɵ�,��֪OD��4,��DC��ȡ��E,DE=8��
��1�������E��O��B����Ĺ��ɵ㣨��E���ڵ�C��, ����OB�ij���
��2�����OB=12���ֱ���OB,ODΪ�����Ὠ����ͼ2��ֱ������ϵ����x����ȡ��F(5��0)�����߶�DC��ȡ��P, ����P��ֱ��l��y�ᣬ��x���ڵ�Q����DP=t��
������P��DE֮�䣬��EFΪֱ����Բ��ֱ��l���У�����t��ֵ��
����ֱ��l��ǡ����2����E��F����Ĺ��ɵ�ʱ��������Ӧt��ȡֵ��Χ��
���𰸡���1��10����2����4����0��t��4��t=5��t=8��9��t��12
��������
��1������OE��BE����OB=x����EC=x-8�������ݹ��ɶ�����ʾ��OE2��BE2��ֵ�������ݹ��ɶ������涨���з�����⼴�ɣ�
��2���ٹ���F��FG��DC������ΪG������M��MN��DE������EFG�����ݹ��ɶ������EF�ij����Ӷ������MH�ij��������ε���λ�߶��������MN�ij���Ȼ������NH=NM-MH�����NH�ij����Ӷ����t��ֵ��
�ڵ�ֱ��l��ԲM�����ֱ��l������E��ֱ��l������Fʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
�⣺��1����ͼ1��ʾ������OE��BE��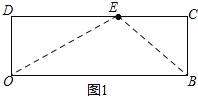
��OB=x����EC=x-8��
����DOE��OE2=DE2+OD2=42+82=80��BE2=CE2+CB2=42+��x-8��2��
��EΪ��O�͵�B�Ĺ��ɶ����㣬
��OB2=OE2+BE2����42+��x-8��2+80=x2��
��ã�x=10��
��OB=10��
��2���ٹ���F��FG��DC������ΪG������M��MN��DE��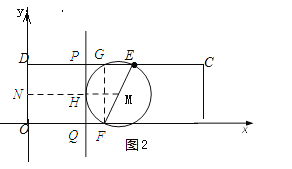
��DE=8��OF=5��DO=4��
��GE=3��FG=4��MN=6.5��
��EF=![]() =5��
=5��
��MH=2.5��
��HN=NM-MH=6.5-2.5=4��
��t=4��
����ͼ3��ʾ����ֱ��l��ԲM����ʱ������E��EG��EF��PQ�ڵ�G������F��HF��EF������ΪH��
�ߡ�GEF=90����
���GEFΪֱ�������Σ�
��G��E��F��һ�����ɵ㣮
ͬ����HҲ��E��F��һ�����ɵ㣮
�൱ֱ��l��ԲM����ʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
�൱0��t��4ʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
ͬ������ֱ��l��ԲM���Ҳֱ࣬��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
��9��t��12��
��ͼ4��ʾ����ֱ��l������Fʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮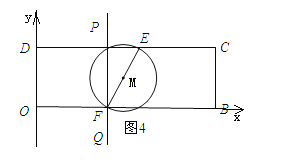
��OF=5��
��t=5��
��ͼ5��ʾ����ֱ��l������Eʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮
��DE=8��
��t=8��
����������0��t��4��t=5��t=8��9��t��12ʱ��ֱ��l��ǡ�ô�����������E��F����Ĺ��ɵ㣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
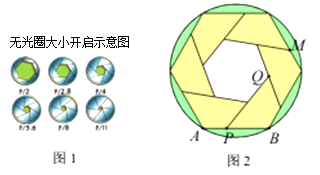
����Ŀ��С������������Ŵ����У���Ȧ��С�仯��ͼ1��ʾ����������������ͼ2��ʾ��ͼ�Σ�ͼ2��������״��С����ͬ���ı���Χ��һ��Բ���ڽ������κ�һ��С�������Σ���PQ���ڵ�ֱ�߾�����M��PB=5cm��С�������ε����Ϊ![]() cm2�����Բ�İ뾶Ϊ________cm��
cm2�����Բ�İ뾶Ϊ________cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
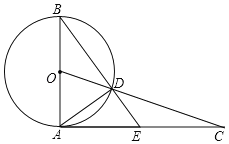
����Ŀ����ͼ��AB�ǡ�O��ֱ��������A����O�����߲�������ȡһ��C������OC����O�ڵ�D��BD���ӳ��߽�AC��E������AD��
��1����֤��CD2��CEAC��
��2����AB��4��AC��4![]() ����AE�ij���
����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���һ�麬��45��ǵ�ֱ�����ǰ���ͼ���ã�ֱ�Ƕ���C������Ϊ��1��0��������A������Ϊ��0��2��������Bǡ�����ڵ�һ����˫�����ϣ��ֽ�ֱ�����ǰ���x��������ƽ�ƣ�������Aǡ�����ڸ�˫������ʱֹͣ�˶������ʱ��C�Ķ�Ӧ��C�������Ϊ��������
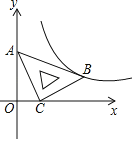
A.��![]() ��0��B.��2��0��C.��
��0��B.��2��0��C.��![]() ��0��D.��3��0��
��0��D.��3��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��3x+3��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵ�һ������������ABCD����D��˫����![]() ��k��0���ϣ�����������x�Ḻ����ƽ��a����λ���Ⱥ�Cǡ�����ڸ�˫�����ϣ���a��ֵ��
��k��0���ϣ�����������x�Ḻ����ƽ��a����λ���Ⱥ�Cǡ�����ڸ�˫�����ϣ���a��ֵ��
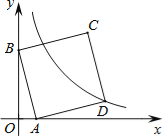
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ƽ�ȫ������ij����ȥ�깺��A��B���ֽ����������ɼ������˽⣬B�ֽ������ĵĵ�����A�ֽ������ĵ�1��5������7200Ԫ����A�ֽ������ı���5400Ԫ����B�ֽ������Ķ�10����
��1��A��B���ֽ������ĵĵ��۷ֱ��Ƕ���Ԫ��
��2�����������ֽ������ĵĵ��ۺ�ȥ�걣�ֲ��䣬�������ƻ��ٹ���A��B���ֽ������Ĺ�50�����ҷ��ò�����21000Ԫ�����ʣ�A�ֽ�����������Ҫ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+3����A(3��0)��B(1��0)����(��ͼ1)������ΪM.
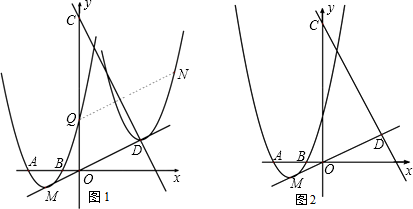
(1)a��b��ֵ��
(2)����������y��Ľ���ΪQ(��ͼ1)��ֱ��y=2x+9��ֱ��OM���ڵ�D. �ֽ�������ƽ�ƣ����ֶ�����ֱ��OD��.�������ߵĶ���ƽ�Ƶ�D��ʱ��Q������N�㣬���������ϵ�����M��Q�����е�����MQɨ��������������
(3)��ֱ��y=2x+9��y�ύ�ڵ�C����ֱ��OM���ڵ�D(��ͼ2).�ֽ�������ƽ�ƣ����ֶ�����ֱ��OD��.��ƽ�Ƶ�������������CD(���˵�C)û�й�����ʱ����̽���䶥��ĺ�����h��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����C���߶�AB�ϣ�����C����A��B�غϣ����ֱ���AC��BCΪ����ABͬ�����ȱ�������ACD�͵ȱ�������BCE������AE��BD���ڵ�P��
���۲���룩
��AE��BD��������ϵ���� ����
�ڡ�APD�Ķ���Ϊ�� ����
����ѧ˼����
��ͼ2������C���߶�AB��ʱ����1���еĽ��ۢ١����Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����
����չӦ�ã�
��ͼ3����EΪ�ı���ABCD��һ�㣬�������AED����BEC��90����AE��DE��BE��CE���Խ���AC��BD���ڵ�P��AC��10�����ı���ABCD�����Ϊ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���![]() ������ʵ����x1��x2��
������ʵ����x1��x2��
��1����ʵ��k��ȡֵ��Χ��
��2���Ƿ����ʵ��kʹ��![]() �����������ڣ������k��ֵ���������ڣ���˵�����ɣ�
�����������ڣ������k��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com