
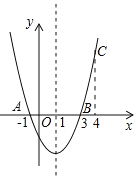
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
【答案】①④
【解析】
利用交点式写出抛物线解析式为y=ax2﹣2ax﹣3a,配成顶点式得y=a(x﹣1)2﹣4a,则可对①进行判断;计算x=4时,y=a51=5a,则根据二次函数的性质可对②进行判断;利用对称性和二次函数的性质可对③进行判断;由于b=﹣2a,c=﹣3a,则方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,然后解方程可对④进行判断.
解:∵二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0),
∴抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∵y=a(x﹣1)2﹣4a,
∴当x=1时,二次函数有最小值﹣4a,所以①正确;
当x=4时,y=a51=5a,
∴当﹣1≤x2≤4,则﹣4a≤y2≤5a,所以②错误;
∵点C(4,5a)关于直线x=1的对称点为(﹣2,5a),
∴当y2>y1,则x2>4或x<﹣2,所以③错误;
∵b=﹣2a,c=﹣3a,
∴方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,
整理得3x2+2x﹣1=0,解得x1=﹣1,x2=![]() ,所以④正确.
,所以④正确.
故答案为①④.


科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
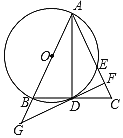
【题目】如图,△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)求证:DF是⊙O的切线;
(2)已知BD=![]() ,CF=2,求DF和BG的长.
,CF=2,求DF和BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
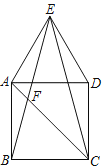
【题目】如图,在正方形ABCD的上方作等边三角形ADE,连接BE,CE.
(1)求证:△ABE≌△DCE;
(2)连接AC,设AC与BE交于点F,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
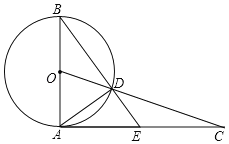
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD,
(1)求证:CD2=CEAC;
(2)若AB=4,AC=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线![]() (k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是
(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是
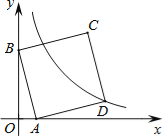
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
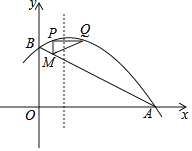
【题目】如图,在平面直角坐标系中,抛物线y=ax2+![]() x+2与x轴交于点A(4,0)与y轴交于点B.点M在线段AB上,其横坐标为m,PM∥y轴,与抛物线交点为点P,PQ∥x轴,与抛物线交点为点Q
x+2与x轴交于点A(4,0)与y轴交于点B.点M在线段AB上,其横坐标为m,PM∥y轴,与抛物线交点为点P,PQ∥x轴,与抛物线交点为点Q
(1)求a的值、并写出此抛物线顶点的坐标;
(2)求m为何值时,△PMQ为等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com