
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:
①△AED≌△DFB;②S四边形 BCDG=![]() CG2;③若AF=2DF,则BG=6GF
CG2;③若AF=2DF,则BG=6GF
,其中正确的结论
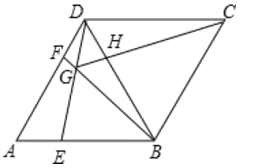
A.只有①②.B.只有①③.C.只有②③.D.①②③.
【答案】D
【解析】
解:①∵ABCD为菱形,∴AB=AD.
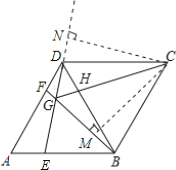
∵AB=BD,∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB;
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
∴CM=CN,
则△CBM≌△CDN,(HL)
∴S四边形BCDG=S四边形CMGN.
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=![]() CG,CM=
CG,CM=![]() CG,
CG,
∴S四边形CMGN=2S△CMG=2×![]() ×
×![]() CG×
CG×![]() CG=
CG=![]() CG2.
CG2.
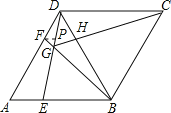
③过点F作FP∥AE于P点.
∵AF=2FD,
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=1:6=FG:BG,
即 BG=6GF.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是抛物线上的动点,且满足
是抛物线上的动点,且满足![]() ,求出
,求出![]() 点的坐标;
点的坐标;
(3)连接![]() ,点
,点![]() 是
是![]() 轴一动点,点
轴一动点,点![]() 是抛物线上一动点,若以
是抛物线上一动点,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,请直接写出点
为顶点的四边形是平行四边形时,请直接写出点![]() 的坐标.
的坐标.
 备用图
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD与正方形DEFG按如图1放置,点A,D,G在同一条直线上,点E在CD边上,AD=3,DE=![]() ,连接AE,CG
,连接AE,CG
(1)线段AE与CC的关系为______;
(2)将正方形DEFG绕点D顺时针旋转一个锐角后,如图2,请问(1)中的结论是否仍然成立?请说明理由
(3)在正方形DEFG绕点D顺时针旋转一周的过程中,当∠AEC=90°时,请直接写出AE的长.
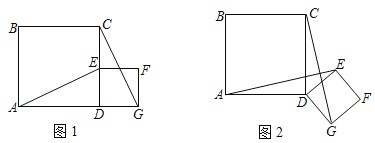
查看答案和解析>>
科目:初中数学 来源: 题型:
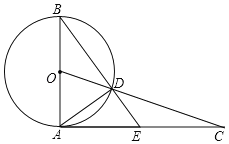
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD,
(1)求证:CD2=CEAC;
(2)若AB=4,AC=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程|x2+2px﹣3p2+5|﹣q=0,其中p、q都是实数.
(1)若q=0时,方程有两个不同的实数根x1x2,且![]() ,求实数p的值.
,求实数p的值.
(2)若方程有三个不同的实数根x1、x2、x3,且![]() ,求实数p和q的值.
,求实数p和q的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
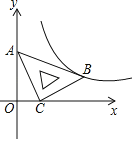
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A.(![]() ,0)B.(2,0)C.(
,0)B.(2,0)C.(![]() ,0)D.(3,0)
,0)D.(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
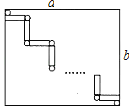
【题目】如图由长为a,宽为b的矩形、(2m+1)个长为4,宽为1的小矩形(为正整数)和若干个小圆组成,其中小圆的直径与小矩形的宽相等.
(1)当m=1时,a= ,b= ;
(2)当a=24时,求b的值;
(3)a的值能否等于30?请通过计算说明理由;
(4)直接写出a与b的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com