
【题目】已知关于x的方程|x2+2px﹣3p2+5|﹣q=0,其中p、q都是实数.
(1)若q=0时,方程有两个不同的实数根x1x2,且![]() ,求实数p的值.
,求实数p的值.
(2)若方程有三个不同的实数根x1、x2、x3,且![]() ,求实数p和q的值.
,求实数p和q的值.
【答案】(1)p=5;(2)![]() ,q=3.
,q=3.
【解析】
(1)根据根与系数的关系可得△=(2p)2﹣4(﹣3p2+5)=16p2﹣20>0,x1+x2=﹣2p,![]() ,代入
,代入![]() 可得关于p的方程,解方程即可;
可得关于p的方程,解方程即可;
(2)由方程有三个不同的实数根x1、x2、x3,可得x3=﹣p,x1、x2是方程x2+2px﹣3p2+5=q的两根;由根与系数的关系可得x1+x2=﹣2p,![]() ,x3=﹣p.△=(2p)2﹣4(﹣7p2+10)=32p2﹣40>0,进而得到关于p的方程,解出p即可求出q的值.
,x3=﹣p.△=(2p)2﹣4(﹣7p2+10)=32p2﹣40>0,进而得到关于p的方程,解出p即可求出q的值.
解:(1)若q=0,则方程为x2+2px﹣3p2+5=0.
因该方程有两个不同的实数x1、x2,
可得△=(2p)2﹣4(﹣3p2+5)=16p2﹣20>0,x1+x2=﹣2p,![]()
解得p2>![]() ;
;
由![]() ,得
,得![]() ,
,
解得p=5或![]() .(注意5﹣3p2≠0)
.(注意5﹣3p2≠0)
因为p2>![]() ,所以p=5.
,所以p=5.
(2)显然q>0.方程可写成x2+2px﹣3p2+5=±q.
因该方程有三个不同的实数根,
即函数![]() 与y2=±q的图象有三个不同的交点,
与y2=±q的图象有三个不同的交点,
∴可得:![]() ,
,
即q=4p2﹣5.x1、x2是方程x2+2px﹣3p2+5=q的两根,
即x2+2px﹣7p2+10=0.
则x1+x2=﹣2p,![]() ,x3=﹣p.
,x3=﹣p.
△=(2p)2﹣4(﹣7p2+10)=32p2﹣40>0,
解得p2>![]() .
.
由![]() ,得
,得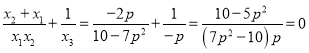 ,
,
解得p2=2>![]() ,
,
所以![]() ,q=4p2﹣5=3.
,q=4p2﹣5=3.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】按如下方法,将△ABC的三边缩小到原来的![]() ,如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
,如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
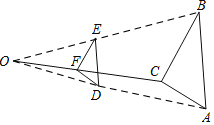
A.点O为位似中心且位似比为1:2
B.△ABC与△DEF是位似图形
C.△ABC与△DEF是相似图形
D.△ABC与△DEF的面积之比为4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:
①△AED≌△DFB;②S四边形 BCDG=![]() CG2;③若AF=2DF,则BG=6GF
CG2;③若AF=2DF,则BG=6GF
,其中正确的结论
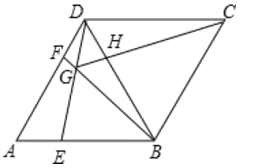
A.只有①②.B.只有①③.C.只有②③.D.①②③.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①c<0;②2a+b=0;③a+b+c<0;④b2﹣4ac<0,其中正确的有( )
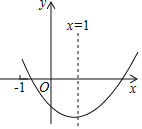
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
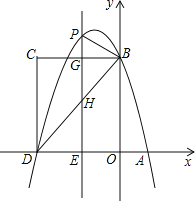
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高速铁路赤峰至喀左段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,下列结论:①
之间,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;其中正确的有( )
;其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com