
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
【答案】(1)100;(2)m=20,补图见解析;(3)36°;(4)250.
【解析】
(1)用“围棋”的人数除以其所占百分比可得;
(2)用总人数乘以“书法”人数所占百分比求得其人数,据此即可补全图形;
(3)用360°乘以“围棋”人数所占百分比即可得;
(4)用总人数乘以样本中“舞蹈”人数所占百分比可得.
(1)学校本次调查的学生人数为10÷10%=100(名).
故答案为:100;
(2)m=100﹣25﹣25﹣20﹣10=20,
∴“书法”的人数为100×20%=20人,
补全图形如下:
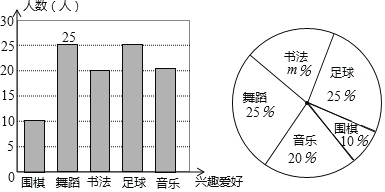
(3)在扇形统计图中,“书法”所在扇形的圆心角度数为360°×10%=36°.
故答案为:36°;
(4)估计该校喜欢舞蹈的学生人数为1000×25%=250人.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的图象经过点
的图象经过点![]() ,交x轴于点A、
,交x轴于点A、![]() 点在B点左侧
点在B点左侧![]() ,顶点为D.
,顶点为D.
![]() 求抛物线的解析式及点A、B的坐标;
求抛物线的解析式及点A、B的坐标;
![]() 将
将![]() 沿直线BC对折,点A的对称点为
沿直线BC对折,点A的对称点为![]() ,试求
,试求![]() 的坐标;
的坐标;
![]() 抛物线的对称轴上是否存在点P,使
抛物线的对称轴上是否存在点P,使![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
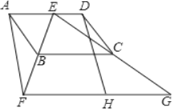
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=60°,∠DCE=20°,求∠CBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=4S△ADF.其中正确的有( )
AE2;④S△ABC=4S△ADF.其中正确的有( )
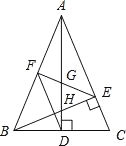
A.1个 B.2 个 C.3 个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,引射线OC(点C在∠AOB外),若∠BOC=α(0°<α<90°),
OD平∠BOC,OE平∠AOD.
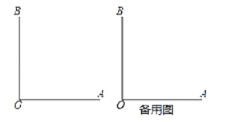
(1)若α=40°,请依题意补全图形,并求∠BOE的度数;
(2)请根据∠BOC=α,求出∠BOE的度数(用含α的表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
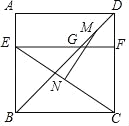
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
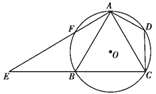
【题目】如图,已知四边形ABCD内接于☉O,A是![]() 的中点,AE⊥AC于A,与☉O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与☉O及CB的延长线交于点F、E,且![]() =
=![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步弘扬中华优秀传统文化,某校决定开展以下四项活动:A经典古诗文朗诵;B书画作品鉴赏;C民族乐器表演;D围棋赛![]() 学校要求学生全员参与,且每人限报一项
学校要求学生全员参与,且每人限报一项![]() 九年级
九年级![]() 班班长根据本班报名结果,绘制出了如下两个尚不完整的统计图,请结合图中信息解答下列问题:
班班长根据本班报名结果,绘制出了如下两个尚不完整的统计图,请结合图中信息解答下列问题: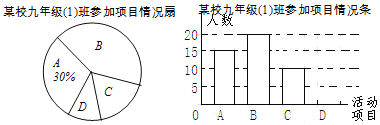
![]() 直接填空:九年级
直接填空:九年级![]() 班的学生人数是______,在扇形统计图中,B项目所对应的扇形的圆心角度数是______;
班的学生人数是______,在扇形统计图中,B项目所对应的扇形的圆心角度数是______;
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 用列表或画树状图的方法,求该班学生小聪和小明参加相同项目活动的概率.
用列表或画树状图的方法,求该班学生小聪和小明参加相同项目活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() (落在矩形
(落在矩形![]() 所在平面内,
所在平面内,![]() 与
与![]() 相交于点
相交于点![]() ,接
,接![]() .
.
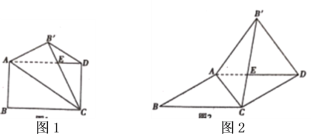
(1)在图1中,
①![]() 和
和![]() 的位置关系为__________________;
的位置关系为__________________;
②将![]() 剪下后展开,得到的图形是_________________;
剪下后展开,得到的图形是_________________;
(2)若图1中的矩形变为平行四边形时(![]() ),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com