
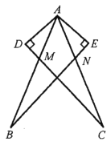
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
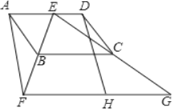
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=60°,∠DCE=20°,求∠CBE的度数.
【答案】(1)证明见解析;
(2)∠CBE=70°.
【解析】
(1)证明AD∥BC,AD=BC,FH∥BC,FH=BC;
(2)∠CBE是等腰△CBE的底角,求出顶角∠ECD即可.
(1)证明:∵BF=BE,CG=CE,
∴BC∥![]() FG,BC=
FG,BC=![]() FG
FG
又∵H是FG的中点,
∴FH∥![]() FG,FH=
FG,FH=![]() FG,
FG,
∴BC∥FH,且BC=FH,
又∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AD∥FH,
∴四边形AFHD是平行四边形;
(2)∵四边形ABCD是平行四边形,∠BAE=60°,
∴∠BAE=∠DCB=60°,
又∵∠DCE=20°,
∴∠ECB=∠DCB-∠DCE=60°-20°=40°,
∵CE=CB,
∴∠CBE=∠BEC=![]() (180°-∠ECB)=
(180°-∠ECB)=![]() (180°-40°)=70°.
(180°-40°)=70°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
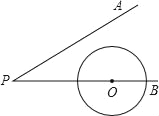
【题目】如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与PA相切时,圆心O平移的距离为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=CD,点M、N分别为AD、BC的中点,点E、F分别是BM、CM的中点.
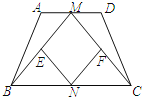
(1)求证:△ABM≌△DCM.
(2)四边形MENF是什么图形?请证明你的结论.
(3)若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.
![]()
(1)计算2⊙(﹣3)的值;
(2)当a,b在数轴上的位置如图所示时,化简a⊙b;
(3)已知(a⊙a)⊙a=8+a,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是AB上的一点,∠COE=90°,OF平分∠AOE.
(1)如图1,当点C,E,F在直线AB的同一侧时,若∠AOC=40°,求∠BOE和∠COF的度数;
(2)在(1)的条件下,∠BOE和∠COF有什么数量关系?请直接写出结论,不必说明理由;
(3)如图2,当点C,E,F分别在直线AB的两侧时,若∠AOC=β,那么(2)中∠BOE和∠COF的数量关系是否仍然成立?请写出结论,并说明理由.
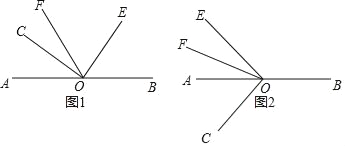
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 和
和![]() 中给出4个论断:①
中给出4个论断:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,
,![]() ;现将4个论断分别粘贴在四个学生的后背上,进行如下游戏:其中三个学生站在讲台的左边,另一个学生站在讲台的右边,要求以三个学生后背上的部分论断作为题设,另一个学生后背上的论断作为结论,使之成为一个真命题或题目,这个游戏可进行几轮?并对其中的一种情况进行证明.
;现将4个论断分别粘贴在四个学生的后背上,进行如下游戏:其中三个学生站在讲台的左边,另一个学生站在讲台的右边,要求以三个学生后背上的部分论断作为题设,另一个学生后背上的论断作为结论,使之成为一个真命题或题目,这个游戏可进行几轮?并对其中的一种情况进行证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com