
����Ŀ����֪��O��AB�ϵ�һ�㣬��COE��90����OFƽ�֡�AOE��
��1����ͼ1������C��E��F��ֱ��AB��ͬһ��ʱ������AOC��40�������BOE�͡�COF�Ķ�����
��2���ڣ�1���������£���BOE�͡�COF��ʲô������ϵ����ֱ��д�����ۣ�����˵�����ɣ�
��3����ͼ2������C��E��F�ֱ���ֱ��AB������ʱ������AOC��������ô��2���С�BOE�͡�COF��������ϵ�Ƿ���Ȼ��������д�����ۣ���˵�����ɣ�
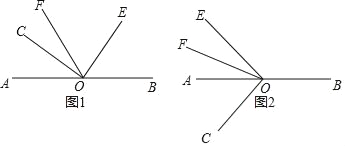
���𰸡�(1) ��COF��25��, ��BOE��50����(2) ��BOE��2��COF;(3) ��BOE��2��COF,���ɼ�����
��������
��1�������BOE�͡�COF�Ķ��������жϣ�
��2���ɣ�1��������⣻
��3�����ۣ���BOE��2��COF�����ݽǵĺͲ�弴�ɽ�����⣮
�⣺��1���ߡ�COE��90������AOC��40����
���BOE��180������AOC����COE��180����40����90����50����
��AOE����AOC+��COE��40��+90����130����
��OFƽ����AOE��
���EOF��![]() ��AOE��
��AOE��![]() ��130����65����
��130����65����
���COF����COE����EOF��90����65����25����
��2����BOE��2��COF��
��3����BOE��2��COF��
�������£��ߡ�COE��90������AOC������
���AOE����COE����AOC��90��������
���BOE��180������AOE��180������90����������90��+����
��OFƽ����AOE��
���AOF��![]() ��AOE��
��AOE��![]() ��90����������45����
��90����������45����![]() ����
����
���COF����+��45����![]() ������45��+
������45��+![]() ����
����
��2��COF��2��45��+![]() ������90��+����
������90��+����
���BOE��2��COF��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
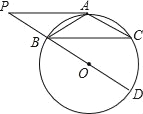
����Ŀ����ͼ����O�У���AΪ![]() �е㣬BDΪֱ������A��AP��BC��DB���ӳ����ڵ�P��
�е㣬BDΪֱ������A��AP��BC��DB���ӳ����ڵ�P��
������֤��PA�ǡ�O�����ߣ�
������BC=2![]() ��AB=2
��AB=2![]() ����sin��ABD��ֵ��
����sin��ABD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�������㷨ͳ�ڡ��У���һ����Ⱥ������������⣬�����ǣ���ͯ���ڲ�ԭ�Ϸ�����ǣ��һֻ���������ʼף��������Ⱥ��100ֻ�����״����������Ⱥ�������ͬ����һȺ���ټ��ϰ�Ⱥ���ķ�֮һȺ���ټ������һֻ������100ֻ��������ͯ���Ŷ���ֻ��������Ⱥ����xֻ�������з����У���ȷ���ǣ�������
A. ��1+![]() +
+![]() ��x=100+1 B. x+x+
��x=100+1 B. x+x+![]() x+
x+![]() x=100��1 C. ��1+
x=100��1 C. ��1+![]() +
+![]() ��x=100��1 D. x+x+
��x=100��1 D. x+x+![]() x+
x+![]() x=100+1
x=100+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��a��b��
��1�����ó߹水����Ҫ����ͼ������Ҫ��д��������Ҫ������ͼ�ۼ���
���ӳ��߶�AB��C��ʹBC��a��
�������ӳ��߶�AB��D��ʹAD��b��
��2���ڣ�1���������£����AB��8cm��a��6m��b��10cm���ҵ�EΪCD���е㣬���߶�AE�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ı���ABCDΪƽ���ı���,EΪAD�ϵ�һ��,����EB���ӳ�,ʹBF=BE,����EC���ӳ�,ʹCG=CE,����FG.HΪFG���е�,����DH.
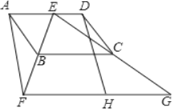
(1)��֤:�ı���AFHDΪƽ���ı���;
(2)��CB=CE,��BAE=60��,��DCE=20��,���CBE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O����֪��BOD��75�㣬OE�ѡ�AOC�ֳ������ǣ��ҡ�AOE����EOC��2��3��
��1�����AOE�Ķ�����
��2����OFƽ�֡�BOE���ʣ�OB�ǡ�DOF��ƽ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BE�Ǹߣ���ABE=45������F��AB���е㣬AD��FE��BE�ֱ��ڵ�G��H����CBE=��BAD�������н��ۣ���FD=FE����AH=2CD����BCAD=![]() AE2����S��ABC=4S��ADF��������ȷ������ ��
AE2����S��ABC=4S��ADF��������ȷ������ ��
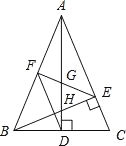
A��1�� B��2 �� C��3 �� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�DZ߳�Ϊ6�������Σ���E�ڱ�AB�ϣ�BE��4������E��EF��BC���ֱ�BD��CD�ڵ�G��F���㣬��M��N�ֱ���DG��CE���е㣬��MN�ij���______��
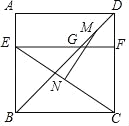
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬AB=3��BC=4.Rt��MPN�У���MPN=90�㣬��P��AC�ϣ�PM��AB�ڵ�E��PN��BC�ڵ�F����PE=2PFʱ��AP=________.
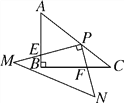
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com