
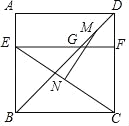
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN的长是______.
【答案】![]()
【解析】
作辅助线,构建矩形MHPK和直角三角形NMH,利用平行线分线段成比例定理或中位线定理得:MK=FK=1,NP=3,PF=2,利用勾股定理可得MN的长.
过M作MK⊥CD于K,过N作NP⊥CD于P,过M作MH⊥PN于H,
则MK∥EF∥NP,
∵∠MKP=∠MHP=∠HPK=90°,
∴四边形MHPK是矩形,
∴MK=PH,MH=KP,
∵NP∥EF,N是EC的中点,
∴![]()
∴PF=![]() FC=
FC=![]() BE=2,NP=
BE=2,NP=![]() EF=3,
EF=3,
同理得:FK=DK=1,
∵四边形ABCD为正方形,
∴∠BDC=45°,
∴△MKD是等腰直角三角形,
∴MK=DK=1,NH=NP﹣HP=3﹣1=2,
∴MH=2+1=3,
在Rt△MNH中,由勾股定理得:MN=![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
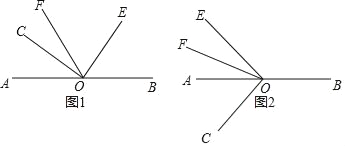
【题目】已知点O是AB上的一点,∠COE=90°,OF平分∠AOE.
(1)如图1,当点C,E,F在直线AB的同一侧时,若∠AOC=40°,求∠BOE和∠COF的度数;
(2)在(1)的条件下,∠BOE和∠COF有什么数量关系?请直接写出结论,不必说明理由;
(3)如图2,当点C,E,F分别在直线AB的两侧时,若∠AOC=β,那么(2)中∠BOE和∠COF的数量关系是否仍然成立?请写出结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD≠BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
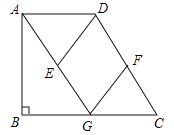
(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.

(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.(![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某销售商计划购进甲、乙两种商品共![]() 件进行销售.已知甲种商品每件进价
件进行销售.已知甲种商品每件进价![]() 元,乙种商品每件进价
元,乙种商品每件进价![]() 元;通过市场考察,销售商决定甲种商品以每件
元;通过市场考察,销售商决定甲种商品以每件![]() 元的价格出售,乙种商品以每件
元的价格出售,乙种商品以每件![]() 元的价格出售.设销售商购进的甲种商品有
元的价格出售.设销售商购进的甲种商品有![]() 件,销售完甲、乙两种商品后获得的总利润为
件,销售完甲、乙两种商品后获得的总利润为![]() 元
元
![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 如果销售商购进的甲种商品的数量不少于乙种商品数量的
如果销售商购进的甲种商品的数量不少于乙种商品数量的![]() 倍,请求出获利最大的进货方案,所获得的最大利润是多少元?
倍,请求出获利最大的进货方案,所获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用大小和形状完全相同的小正方体木块搭成一-个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
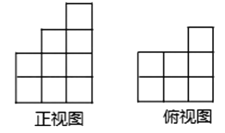
A.22个B.19个C.16个D.13个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com