
【题目】对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.
![]()
(1)计算2⊙(﹣3)的值;
(2)当a,b在数轴上的位置如图所示时,化简a⊙b;
(3)已知(a⊙a)⊙a=8+a,求a的值.
【答案】(1)2⊙(﹣3)=6;(2)a⊙b=﹣2b;(3)当a≥0时, a=![]() ;当a<0时, a=﹣
;当a<0时, a=﹣![]() .
.
【解析】
(1)根据文中的新运算法则将2⊙(﹣3)转化为我们熟悉的计算方式进行计算即可;
(2)根据文中的新运算法则将a⊙b转化为|a+b|+|a﹣b|,然后先判断出a+b与a﹣b的正负性,之后利用绝对值代数意义化简即可;
(3)先根据文中的新运算法则将(a⊙a)⊙a转化为我们熟悉的计算方式,此时注意对a进行分a≥0、a<0两种情况讨论,然后得出新的方程求解即可.
(1)由题意可得:2⊙(﹣3)=|2﹣3|+|2+3|=6;
(2)由数轴可知,a+b<0,a﹣b>0,
∴a⊙b=|a+b|+|a﹣b|=﹣a﹣b+a﹣b=﹣2b;
(3)当a≥0时,(a⊙a)⊙a=2a⊙a=4a=8+a,
∴a=![]() ;
;
当a<0时,(a⊙a)⊙a=(﹣2a)⊙a=﹣4a=8+a,
∴a=![]() .
.
综上所述,a的值为![]() 或
或![]() .
.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】同学们,我们知道图形是由点、线、面组成,结合具体实例,已经感受到“点动成线,线动成面”的现象,下面我们一起来进一步探究:
(概念认识)
已知点P和图形M,点B是图形M上任意一点,我们把线段PB长度的最小值叫做点P与图形M之间的距离.
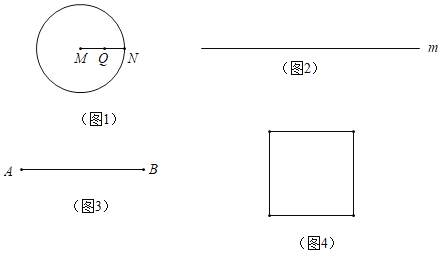
例如,以点M为圆心,1cm为半径画圆如图1,那么点M到该圆的距离等于1cm;若点N是圆上一点,那么点N到该圆的距离等于0cm;连接MN,若点Q为线段MN中点,那么点Q到该圆的距离等于0.5cm,反过来,若点P到已知点M的距离等于1cm,那么满足条件的所有点P就构成了以点M为圆心,1cm为半径的圆.
(初步运用)
(1)如图2,若点P到已知直线m的距离等于1cm,请画出满足条件的所有点P.
(深入探究)
(2)如图3,若点P到已知线段的距离等于1cm,请画出满足条件的所有点P.
(3)如图4,若点P到已知正方形的距离等于1cm,请画出满足条件的所有点P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知О是直线AB上的一点,![]() ,OE平分
,OE平分![]() .
.
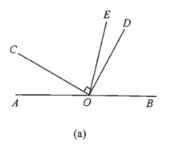
(1)在图(a)中,若![]() ,求
,求![]() 的度数;
的度数;
(2)在图(a)中,若![]() ,直接写出
,直接写出![]() 的度数(用含
的度数(用含![]() 的代数式表示)
的代数式表示)
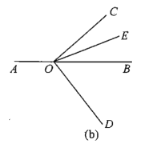
(3)将图(a)中的![]() 绕顶点O顺时针旋转至图(b)的位置.
绕顶点O顺时针旋转至图(b)的位置.
①探究![]() 和
和![]() 的度数之间的关系,直接写出结论;
的度数之间的关系,直接写出结论;
②在![]() 的内部有一条射线OF,满足:
的内部有一条射线OF,满足:![]() ,试确定
,试确定![]() 与
与![]() 的度数之间的关系,并说明理由.
的度数之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的圆F切DC于点E. 若圆F的半径是6cm,AD=4cm,求梯形ABCD的面积.
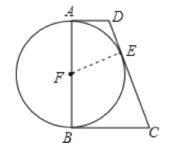
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
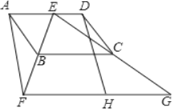
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=60°,∠DCE=20°,求∠CBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式.(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,引射线OC(点C在∠AOB外),若∠BOC=α(0°<α<90°),
OD平∠BOC,OE平∠AOD.
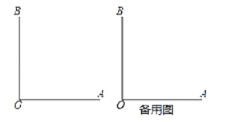
(1)若α=40°,请依题意补全图形,并求∠BOE的度数;
(2)请根据∠BOC=α,求出∠BOE的度数(用含α的表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com