
【题目】如图,在平面直角坐标系中,抛物线![]() 的图象经过点
的图象经过点![]() ,交x轴于点A、
,交x轴于点A、![]() 点在B点左侧
点在B点左侧![]() ,顶点为D.
,顶点为D.
![]() 求抛物线的解析式及点A、B的坐标;
求抛物线的解析式及点A、B的坐标;
![]() 将
将![]() 沿直线BC对折,点A的对称点为
沿直线BC对折,点A的对称点为![]() ,试求
,试求![]() 的坐标;
的坐标;
![]() 抛物线的对称轴上是否存在点P,使
抛物线的对称轴上是否存在点P,使![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】![]()
![]() ,
,![]() A′(1,4);
A′(1,4);![]() P的坐标为
P的坐标为![]() 或
或![]()
【解析】分析:(1)将(0,2)代入抛物线解析式求得a的值,从而得出抛物线的解析式,再令y=0,得出x的值,即可求得点A、B的坐标;
(2)如图2,作A'H⊥x轴于H,可证明△AOC∽△COB,得出∠ACO=∠CBO,由A'H∥OC,即可得出A′H的长,即可求得A′的坐标;
(3)分两种情况:①如图3,以AB为直径作⊙M,⊙M交抛物线的对称轴于P(BC的下方),由圆周角定理得出点P坐标;②如图4,类比第(2)小题的背景将△ABC沿直线BC对折,点A的对称点为A',以A'B为直径作⊙M',⊙M'交抛物线的对称轴于P'(BC的上方),作M'E⊥A'H于E,交对称轴于F,求得M'F,在Rt△M'P'F中,由勾股定理得出P'F得的长,从而得出点P的坐标即可.
详解:(1)把C(0,2)代入y=ax2-3ax-4a得-4a=2,
解得a=![]() .
.
所以抛物线的解析式为y=![]() x2+
x2+![]() x+2.
x+2.
令![]() x2+
x2+![]() x+2=0,可得:x1=-1,x2=4.
x+2=0,可得:x1=-1,x2=4.
所以A(-1,0),B(4,0).
(2)如图2,作A'H⊥x轴于H,
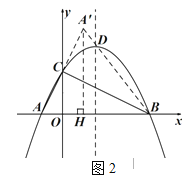
因为![]() ,且∠AOC=∠COB=90°,
,且∠AOC=∠COB=90°,
所以△AOC∽△COB,
所以∠ACO=∠CBO,可得∠ACB=∠OBC+∠BCO=90°,
由A'H∥OC,AC=A'C得OH=OA=1,A'H=2OC=4;
所以A'(1,4);
(3)分两种情况:
①如图3,以AB为直径作⊙M,⊙M交抛物线的对称轴于P(BC的下方),
由圆周角定理得∠CPB=∠CAB,
易得:MP=![]() AB.所以P(
AB.所以P(![]() ,
,![]() ).
).

②如图4,类比第(2)小题的背景将△ABC沿直线BC对折,

点A的对称点为A',以A'B为直径作⊙M',⊙M'交抛物线的对称轴于P'(BC的上方),
则∠CP2B=∠CA'B=∠CAB.
作M'E⊥A'H于E,交对称轴于F.
则M'E=![]() BH=
BH=![]() ,EF=
,EF=![]() 1=
1=![]() .
.
所以M'F=![]()
![]() =1.
=1.
在Rt△M'P'F中,P'F=![]() =
=![]() ,
,
所以P'M=2+![]() .
.
所以P'(![]() ,2+
,2+![]() ).
).
综上所述,P的坐标为(![]() ,
,![]() )或(
)或(![]() ,2+
,2+![]() ).
).


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
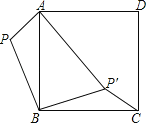
A.105° B.112.5° C.120° D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知О是直线AB上的一点,![]() ,OE平分
,OE平分![]() .
.
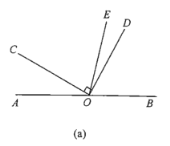
(1)在图(a)中,若![]() ,求
,求![]() 的度数;
的度数;
(2)在图(a)中,若![]() ,直接写出
,直接写出![]() 的度数(用含
的度数(用含![]() 的代数式表示)
的代数式表示)
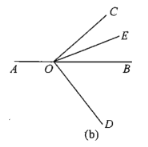
(3)将图(a)中的![]() 绕顶点O顺时针旋转至图(b)的位置.
绕顶点O顺时针旋转至图(b)的位置.
①探究![]() 和
和![]() 的度数之间的关系,直接写出结论;
的度数之间的关系,直接写出结论;
②在![]() 的内部有一条射线OF,满足:
的内部有一条射线OF,满足:![]() ,试确定
,试确定![]() 与
与![]() 的度数之间的关系,并说明理由.
的度数之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从数轴上的原点开始,先向左移动2cm到达A点,再向左移动4cm到达B点,然后向右移动10cm到达C点.
![]()
(1)用1个单位长度表示1cm,请你在题中所给的数轴上表示出A、B、C三点的位置;
(2)把点C到点A的距离记为CA,则CA=______cm;
(3)若点B以每秒3cm的速度向左移动,同时A、C点以每秒lcm、5cm的速度向右移动,设移动时间为t(t>0)秒,试探究CA﹣AB的值是否会随着t的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
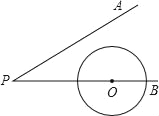
【题目】如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与PA相切时,圆心O平移的距离为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=CD,点M、N分别为AD、BC的中点,点E、F分别是BM、CM的中点.
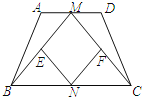
(1)求证:△ABM≌△DCM.
(2)四边形MENF是什么图形?请证明你的结论.
(3)若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com