
【题目】已知О是直线AB上的一点,![]() ,OE平分
,OE平分![]() .
.
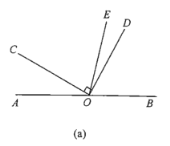
(1)在图(a)中,若![]() ,求
,求![]() 的度数;
的度数;
(2)在图(a)中,若![]() ,直接写出
,直接写出![]() 的度数(用含
的度数(用含![]() 的代数式表示)
的代数式表示)
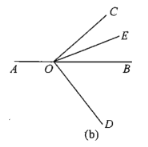
(3)将图(a)中的![]() 绕顶点O顺时针旋转至图(b)的位置.
绕顶点O顺时针旋转至图(b)的位置.
①探究![]() 和
和![]() 的度数之间的关系,直接写出结论;
的度数之间的关系,直接写出结论;
②在![]() 的内部有一条射线OF,满足:
的内部有一条射线OF,满足:![]() ,试确定
,试确定![]() 与
与![]() 的度数之间的关系,并说明理由.
的度数之间的关系,并说明理由.
【答案】(1)15°;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度数;
(2)由(1)中的证明方法可得出结论∠DOE=![]() ∠AOC,从而用含
∠AOC,从而用含![]() 的代数式表示出∠DOE的度数;
的代数式表示出∠DOE的度数;
(3)①由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),从而得出∠AOC和∠DOE的度数之间的关系;
②设![]() ,
,![]() ,根据①中结论以及已知
,根据①中结论以及已知![]() ,得出
,得出![]() ,从而得出结论.
,从而得出结论.
(1)∵![]() ,
,![]() ,
,
∴![]() .
.
∵OE平分![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]()
(2)![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵OE平分![]() ,
,
∴ ![]()
∵![]() ,
,
∴![]() .
.
(3)①![]() .
.
∵OE平分![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
即![]() .
.
②![]() .
.
理由:设![]() ,
,![]() ,
,
由①可知,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
即![]() .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后,分别位于点Q、R处,且相距30海里,如果知道“远航”号沿北偏东![]() 方向航行,请求出“海天”号的航行方向?
方向航行,请求出“海天”号的航行方向?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把 6个相同的小正方体摆成如图的几何体.
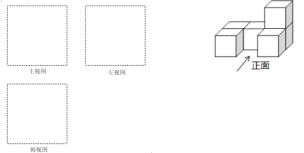
(1)画出该几何体的主视图、左视图、俯视图;
(2)如果每个小正方体棱长为![]() ,则该几何体的表面积是
,则该几何体的表面积是 ![]() .
.
(3)如果在这个几何体上再添加一些相同的小正方体,并并保持左视图和俯视图不变,那么最多可以再 添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
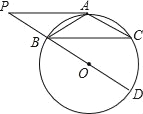
【题目】如图,⊙O中,点A为![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
(Ⅰ)求证:PA是⊙O的切线;
(Ⅱ)若BC=2![]() ,AB=2
,AB=2![]() ,求sin∠ABD的值.
,求sin∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过画图,寻找对顶角和邻补角(不含平角):
(1)若2条直线相交于一点,则有_____________对对顶角,_____________对邻补角.
(2)若3条直线相交于同一点,则有_____________对对顶角,_____________对邻补角.
(3)若4条直线相交于同一点,则有______________对对顶角,__________________对邻补角.
(4)通过(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于同一点,则可形成___________对对顶角,___________对邻补角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六![]() 一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
![]() 求A、B两种品牌服装每套进价分别为多少元?
求A、B两种品牌服装每套进价分别为多少元?
![]() 该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的图象经过点
的图象经过点![]() ,交x轴于点A、
,交x轴于点A、![]() 点在B点左侧
点在B点左侧![]() ,顶点为D.
,顶点为D.
![]() 求抛物线的解析式及点A、B的坐标;
求抛物线的解析式及点A、B的坐标;
![]() 将
将![]() 沿直线BC对折,点A的对称点为
沿直线BC对折,点A的对称点为![]() ,试求
,试求![]() 的坐标;
的坐标;
![]() 抛物线的对称轴上是否存在点P,使
抛物线的对称轴上是否存在点P,使![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中,有一道“群羊逐草”的问题,大意是:牧童甲在草原上放羊,乙牵着一只羊来,并问甲:“你的羊群有100只吗?”甲答:“如果在这群羊里加上同样的一群,再加上半群,四分之一群,再加上你的一只,就是100只.”问牧童甲赶着多少只羊?若设这群羊有x只,则下列方程中,正确的是( )
A. (1+![]() +
+![]() )x=100+1 B. x+x+
)x=100+1 B. x+x+![]() x+
x+![]() x=100﹣1 C. (1+
x=100﹣1 C. (1+![]() +
+![]() )x=100﹣1 D. x+x+
)x=100﹣1 D. x+x+![]() x+
x+![]() x=100+1
x=100+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=4S△ADF.其中正确的有( )
AE2;④S△ABC=4S△ADF.其中正确的有( )
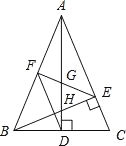
A.1个 B.2 个 C.3 个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com