
【题目】把 6个相同的小正方体摆成如图的几何体.
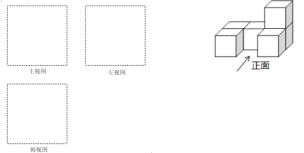
(1)画出该几何体的主视图、左视图、俯视图;
(2)如果每个小正方体棱长为![]() ,则该几何体的表面积是
,则该几何体的表面积是 ![]() .
.
(3)如果在这个几何体上再添加一些相同的小正方体,并并保持左视图和俯视图不变,那么最多可以再 添加 个小正方体.
科目:初中数学 来源: 题型:
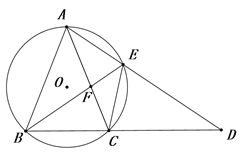
【题目】如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
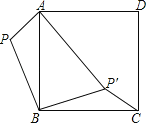
A.105° B.112.5° C.120° D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
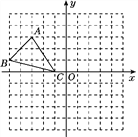
【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
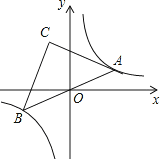
【题目】如图,点A是双曲线y=![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,OC、OD是两条射线,OC⊥OD,射线OE平分∠BOC.
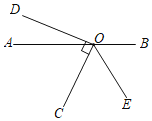
(1)若∠DOE=150°,求∠AOC的度数.
(2)若∠DOE=α,则∠AOC= .(请用含α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知О是直线AB上的一点,![]() ,OE平分
,OE平分![]() .
.
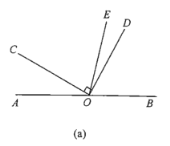
(1)在图(a)中,若![]() ,求
,求![]() 的度数;
的度数;
(2)在图(a)中,若![]() ,直接写出
,直接写出![]() 的度数(用含
的度数(用含![]() 的代数式表示)
的代数式表示)
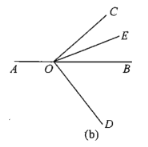
(3)将图(a)中的![]() 绕顶点O顺时针旋转至图(b)的位置.
绕顶点O顺时针旋转至图(b)的位置.
①探究![]() 和
和![]() 的度数之间的关系,直接写出结论;
的度数之间的关系,直接写出结论;
②在![]() 的内部有一条射线OF,满足:
的内部有一条射线OF,满足:![]() ,试确定
,试确定![]() 与
与![]() 的度数之间的关系,并说明理由.
的度数之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=CD,点M、N分别为AD、BC的中点,点E、F分别是BM、CM的中点.
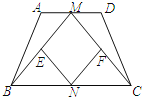
(1)求证:△ABM≌△DCM.
(2)四边形MENF是什么图形?请证明你的结论.
(3)若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com