练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．下列图形中，不是轴对称图形的是（　　）
    A．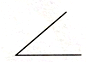
    锐角    		B．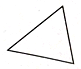
    等腰三角形    		C．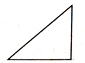
    直角三角形    		D．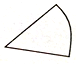
    扇形

    分析 根据关于某条直线对称的图形叫轴对称图形，进而判断得出即可．

    解答 解：A、角是轴对称图形，不合题意；
    B、等腰三角形是轴对称图形，不合题意；
    C、直角三角形不是轴对称图形，符合题意；
    D、扇形是轴对称图形，不合题意；
    故选：C．

    点评 此题主要考查了轴对称图形，轴对称图形的关键是寻找对称轴，对称轴可使图形两部分折叠后重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

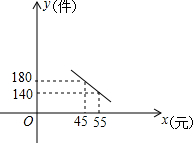    2．大学生王强积极响应“自主创业”的好种，准备投资销售一种进价为每件4元的小家电，通过试营销发现，当销售单价在40元至60元之间（含40元和60元）时，每月的销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数，其图象如图所示．
    （1）求y与x的函数关系式．
    （2）设王强每月获得的利润为p（元），求p与x之间的函数关系式；如果王强想要每月获得最大的利润，那么销售单价应定为多少元？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．在菱形ABCD中，∠BAD=60°，AB=1，此时称为图形L（1），连接图形L（1）的各边中点，得图形J（1），再连接图形J（1）各边中点得图形L（2），在连接图形L（2）各边中点得图形J（2），以此类推…，则图形L（n）的边长与图形J（n）的宽的和是$\frac{3}{{2}^{n}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图1，在△ABC中，∠C=90°，点D在AC上，且CD＞DA，DA=2，点P，Q同时从点D出发，以相同的速度分别沿射线DC、射线DA运动，过点Q作AC的垂线段QR，使QR=PQ，连接PR，当点Q到达点A时，点P，Q同时停止运动．设PQ=x，△PQR与△ABC重叠部分的面积为S，S关于x的函数图象如图2所示（其中0＜x≤$\frac{8}{7}$，$\frac{8}{7}$＜x≤m时，函数的解析式不同）．
    （1）填空：n的值为$\frac{32}{49}$；
    （2）求S关于x的函数关系式，并写出x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为Pn，则点P3的坐标是（8，3）；点P2015的坐标是（1，4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知方程$\frac{1}{x-1}$=$\frac{a}{x+1}$的解为x=2，先化简（1-$\frac{1}{a-1}$）+$\frac{{a}^{2}-4a+4}{{a}^{2}-1}$，再求它的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列各数中，是无理数的是（　　）
    A．-$\frac{1}{3}$B．（-π）0C．sin60°D．$\root{3}{8}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

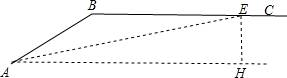    1．某乡间公路有一斜坡AB的坡角为24°36′（即∠BAH=24°36′），斜坡AB的长为100m，路面BC是一段平路，现政府决定把斜坡AB改造成了坡角为12°的斜坡路AE（如图）．
    （1）求斜坡路AE垂直高度（即EH的长）；
    （2）坡路AE比坡路AB增加了多少米？（有关三角函数值用计算器计算，或直接用sin24°36′=0.416，cos24°36′=0.9092，tan24°36′=0.4578，sin12°=0.208，cos12°=0.978，tan12°=0.213，最后结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

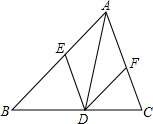    2．如图，已知AD是△ABC的角平分线，点E、F分别是边AC、AB的中点，连接DE、DF，要使四边形AEDF称为菱形，还需添加一个条件，这个条件可以是AB=AC、∠B=∠C或AE=AF（答案不唯一）．．

    查看答案和解析>>

    同步练习册答案