
分析 连接BD,由菱形的性质得出AB=AD,证明△ABD是等边三角形,得出BD=AB=1,证明EH是△ABD的中位线,得出EH=$\frac{1}{2}$BD=$\frac{1}{2}$,得出AB+EH=$\frac{3}{2}$,同理:MN=$\frac{1}{2}$AB=$\frac{1}{2}$,RT=$\frac{1}{4}$,得出MN+RT=$\frac{3}{{2}^{2}}$,…,得出规律:图形L(n)的边长与图形J(n)的宽的和=$\frac{1}{{2}^{n-1}}$+$\frac{1}{{2}^{n}}$=$\frac{3}{{2}^{n}}$.
解答 解:连接BD,如图所示: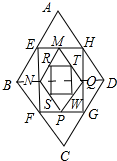 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=1,
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线,
∴EH=$\frac{1}{2}$BD=$\frac{1}{2}$,
∴AB+EH=1+$\frac{1}{2}$=$\frac{3}{2}$,
同理:MN=$\frac{1}{2}$AB=$\frac{1}{2}$,RT=$\frac{1}{4}$,
∴MN+RT=$\frac{1}{2}$+$\frac{1}{4}$=$\frac{3}{4}$=$\frac{3}{{2}^{2}}$,…,
图形L(n)的边长与图形J(n)的宽的和=$\frac{1}{{2}^{n-1}}$+$\frac{1}{{2}^{n}}$=$\frac{3}{{2}^{n}}$;
故答案为:$\frac{3}{{2}^{n}}$.
点评 本题考查了菱形的性质、等边三角形的判定与性质、三角形中位线定理;熟练掌握菱形的性质,根据题意得出规律是解决问题的关键.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
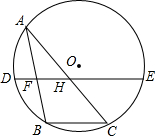 如图,点A是⊙O上一动点,BC是⊙O的一条弦,且∠BAC=30°,点F、H分别是AB、AC的中点,直线FH与⊙O交于D、E两点.若DF+EH的最大值是12,则⊙O的半径是8.
如图,点A是⊙O上一动点,BC是⊙O的一条弦,且∠BAC=30°,点F、H分别是AB、AC的中点,直线FH与⊙O交于D、E两点.若DF+EH的最大值是12,则⊙O的半径是8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
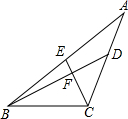 已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )| A. | $\frac{16}{3}$ | B. | 8 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
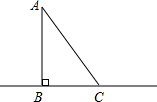 如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB=11.9m(用计算器计算,结果精确到0.1米)
如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB=11.9m(用计算器计算,结果精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com