
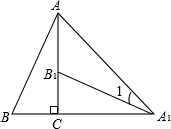
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是60°.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连结AA1,若∠AA1B1=15°,则∠B的度数是60°. 分析 根据旋转的性质可得AC=A1C,然后判断出△ACA1是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA1=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A1B1C,然后根据旋转的性质可得∠B=∠A1B1C.
解答 解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A1B1C,
∴AC=A1C,
∴△ACA1是等腰直角三角形,
∴∠CAA1=15°,
∴∠A1B1C=∠1+∠CAA1=15°+45°=60°,
由旋转的性质得∠B=∠A1B1C=60°,
故答案为60°.
点评 本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.


科目:初中数学 来源: 题型:解答题
 定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.
定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
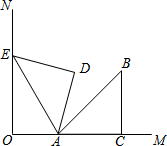 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.
如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
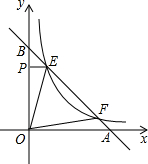 如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.
如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
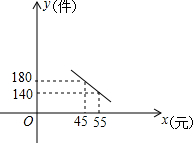 大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com