
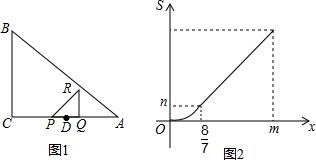
���� ��1����x=$\frac{8}{7}$ʱ����PQR���ABC�ص����ֵ�������ǡ�PQR�������Ȼ�����PQ=$\frac{8}{7}$��QR=PQ�����n��ֵ�Ƕ��ټ��ɣ�
��2�����ȸ���S����x�ĺ���ͼ�ɵ�S����x�ĺ�������ʽ�������������0��x��$\frac{8}{7}$ʱ��S=$\frac{1}{2}$��PQ��RQ=$\frac{1}{2}$x2���жϳ�����Q���˶�����Aʱ��x=2AD=4���ݴ����m=4��Ȼ�������$\frac{8}{7}$��x��4ʱ��S����x�ĺ�����ϵʽ���ɣ�
��� �⣺��1����ͼ1��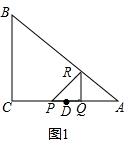 ��
��
��x=$\frac{8}{7}$ʱ����PQR���ABC�ص����ֵ�������ǡ�PQR�������
��PQ=$\frac{8}{7}$��QR=PQ��
��QR=$\frac{8}{7}$��
��n=S=$\frac{1}{2}$����$\frac{8}{7}$��2=$\frac{1}{2}$��$\frac{64}{49}$=$\frac{32}{49}$��
��2����ͼ2��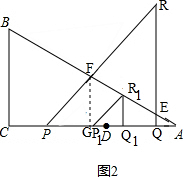 ��
��
����S����x�ĺ���ͼ�ɵ�S����x�ĺ�������ʽ�����������
��0��x��$\frac{8}{7}$ʱ��
S=$\frac{1}{2}$��PQ��RQ=$\frac{1}{2}$x2��
����Q���˶�����Aʱ��
x=2AD=4��
��m=4��
��$\frac{8}{7}$��x��4ʱ��
S=S��APF-S��AQE=$\frac{1}{2}$AP•FG-$\frac{1}{2}$AQ•EQ��
AP=2+$\frac{x}{2}$��AQ=2-$\frac{x}{2}$��
�ߡ�AQE�ס�AQ1R1��$\frac{AQ}{{AQ}_{1}}=\frac{QE}{{{Q}_{1}R}_{1}}$��
��QE=$\frac{4}{5}��2-\frac{x}{2}��$��
��FG=PG=a��
�ߡ�AGF�ס�AQ1R1��$\frac{AG}{{AQ}_{1}}=\frac{FG}{{{Q}_{1}R}_{1}}$��
��AG=2+$\frac{x}{2}$-a��
$\frac{2+\frac{x}{2}-a}{\frac{10}{7}}=\frac{a}{\frac{8}{7}}$
��a=$\frac{4}{9}��2+\frac{x}{2}��$��
��S=S��APF-S��AQE
=$\frac{1}{2}$AP•FG-$\frac{1}{2}$AQ•EQ
=$\frac{1}{2}$��2$+\frac{x}{2}$��$•\frac{4}{9}$��2$+\frac{x}{2}$��-$\frac{1}{2}$��2-$\frac{x}{2}$��•$\frac{4}{5}$��2$-\frac{x}{2}$��
=-$\frac{2}{45}$x2+$\frac{56}{45}x$$-\frac{32}{45}$
��S=-$\frac{2}{45}$x2+$\frac{56}{45}x$$-\frac{32}{45}$��
���ϣ��ɵ�
S=$\left\{\begin{array}{l}{{\frac{1}{2}x}^{2}��0��x��\frac{8}{7}}\\{-{\frac{2}{45}x}^{2}+\frac{56}{45}x-\frac{32}{45}��\frac{8}{7}��x��4}\end{array}\right.$
�ʴ�Ϊ��$\frac{32}{49}$��
���� ������Ҫ�����˶�������ĺ���ͼ��Ҫ�������գ�������Ĺؼ���Ҫ��ȷ��ͼ��Ӧ����Ϣ�㷺��ͨ����ͼ��ȡ��Ϣ���������Խ�������е�ʵ�����⣬��������߷������⡢����������������ͼ��������ʱ��Ҫ����ͼ��ĺ��弴��ʶͼ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2x-1 | B�� | y=$\frac{3}{x}$ | C�� | y=2x | D�� | y=$\frac{2}{x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
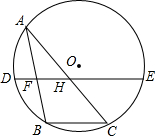 ��ͼ����A�ǡ�O��һ���㣬BC�ǡ�O��һ���ң��ҡ�BAC=30�㣬��F��H�ֱ���AB��AC���е㣬ֱ��FH���O����D��E���㣮��DF+EH�����ֵ��12�����O�İ뾶��8��
��ͼ����A�ǡ�O��һ���㣬BC�ǡ�O��һ���ң��ҡ�BAC=30�㣬��F��H�ֱ���AB��AC���е㣬ֱ��FH���O����D��E���㣮��DF+EH�����ֵ��12�����O�İ뾶��8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
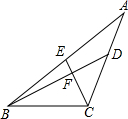 ��֪��ABC�У�D��E�ֱ���AC��AB���ϵ��е㣬BD��CE�ڵ�F��CE=2��BD=4�����ABC�����Ϊ��������
��֪��ABC�У�D��E�ֱ���AC��AB���ϵ��е㣬BD��CE�ڵ�F��CE=2��BD=4�����ABC�����Ϊ��������| A�� | $\frac{16}{3}$ | B�� | 8 | C�� | 4 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 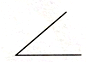 ��� | B�� | 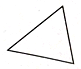 ���������� | C�� | 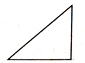 ֱ�������� | D�� |  ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
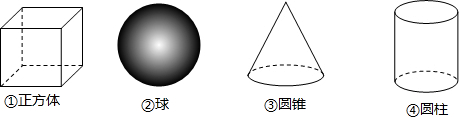
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com