
【题目】如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
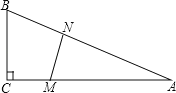
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
【答案】(1)4(2)当t=6时,△AMN的面积最大,最大值为![]()
【解析】解:(1)∵从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒,运动时间为t秒,
∴AM=12﹣t,AN=2t。
∵∠AMN=∠ANM,∴AM=AN,即12﹣t=2t,解得:t=4 秒。
∴当t为4时,∠AMN=∠ANM。
(2)如图作NH⊥AC于H,
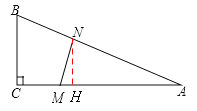
∴∠NHA=∠C=90°。∴NH∥BC。
∴△ANH∽△ABC。
∴![]() ,即
,即![]() 。∴NH=
。∴NH=![]() 。
。
∴![]() 。
。
∴当t=6时,△AMN的面积最大,最大值为![]() 。
。
(1)用t表示出AM和AN的值,根据AM=AN,得到关于t的方程求得t值即可。
(2)作NH⊥AC于H,证得△ANH∽△ABC,从而得到比例式,然后用t表示出NH,从而计算其面积得到有关t的二次函数求最值即可。


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=8,AD=10,点E为BC上一点,将△ABE沿AE折叠,使点B落在长方形内点F处,且DF=6.
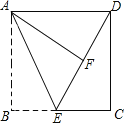
(1)试说明:△ADF是直角三角形;
(2)求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的顶点都在正方形网格的格点上,点
的顶点都在正方形网格的格点上,点![]()
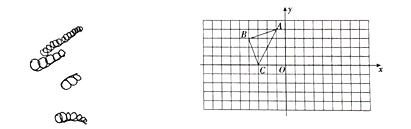
(1)作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,点
,点![]() 的对应点
的对应点![]() 的坐标为___________.
的坐标为___________.
(2)作出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,点
,点![]() 的对应点
的对应点![]() 的坐标为__________.
的坐标为__________.
(3)观察图形,说一说点![]() 和点
和点![]() 的坐标有什么特点.
的坐标有什么特点.
查看答案和解析>>
科目:初中数学 来源: 题型:
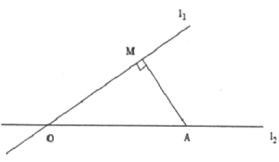
【题目】如图,两条公路![]() 、
、![]() 交予点
交予点![]() ,在公路
,在公路![]() 旁有一学校
旁有一学校![]() ,与
,与![]() 点的距离为
点的距离为![]() ,点
,点![]() (学校)到公路
(学校)到公路![]() 的距离
的距离![]() 为
为![]() .一大货车从
.一大货车从![]() 点出发,行驶在公路
点出发,行驶在公路![]() 上,汽车周围
上,汽车周围![]() 范围内有噪音影响.
范围内有噪音影响.
(1)货车开过学校是否受噪音影响?为什么?
(2)若汽车速度为![]() ,则学校受噪音影响多少秒钟?
,则学校受噪音影响多少秒钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
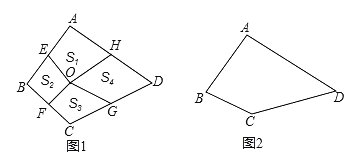
【题目】定义:我们把对角线互相垂直的四边形叫做和美四边形,对角线交点称为和美四边形的中心.
(1)写出一种你学过的和美四边形_________;
(2)如图1,点O是和美四边形ABCD的中心,E,F,G、H分别是边AB,BC,CD,DA的中点,连接OE,OF,OG,OH,记四边形AEOH,BEOF,CGOF,DHOG的面积为![]() ,用等式表示
,用等式表示![]() 的数量关系(无需说明理由).
的数量关系(无需说明理由).
(3)如图2,四边形ABCD是和美四边形,若AB=3,BC=2,CD=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学试验(用纸签D、E、F表示)中各抽取一个实验操作进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com