
【题目】《九章算术》是我国古代内容极为丰富的数学名著。书中有下列问题“今有勾八步,股十五步。问勾中容圆径几何?”其意思为今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是步。
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
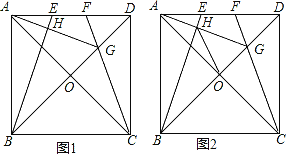
(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个多面体的表面展开图,每个面上都标注了字母(字母在多面体的外表面),请根据要求回答问题.

(1)如果D面在多面体的左面,那么F面在哪里?
(2)B面和哪一面是相对的面?
(3)如果C面在前面,从上面看到的是D面,那么从左面能看到哪一面?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BD上有一点C,则:
(1)∠1和∠ABC是直线AB,CE被直线_____所截得的____角;
(2)∠2和∠BAC是直线CE,AB被直线____所截得的_____角;
(3)∠3和∠ABC是直线_____、_____被直线_____所截得的____角;
(4)∠ABC和∠ACD是直线____、_____被直线_____所截得的角;
(5)∠ABC和∠BCE是直线_____、______被直线所截得的_____角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P以每秒2㎝的速度沿图甲的边框按从![]() 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:

(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙的b是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线 ![]() (k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( )
(k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( ) 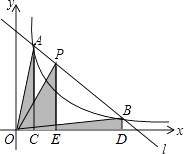
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com