
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
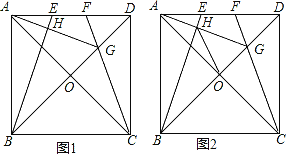
(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
【答案】(1)证明见解析(2)AG⊥BE(3)证明见解析
【解析】
(1)根据正方形的性质得DA=DC,∠ADB=∠CDB=45°,则可根据“SAS”证明△ADG≌△CDG,所以∠DAG=∠DCG;
(2)根据正方形的性质得AB=DC,∠BAD=∠CDA=90°,根据“SAS”证明△ABE≌△DCF,则∠ABE=∠DCF,由于∠DAG=∠DCG,所以∠DAG=∠ABE,然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°,于是可判断AG⊥BE;
(3)如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,证明△AON≌△BOM,可得四边形OMHN为正方形,因此HO平分∠BHG结论成立.
(1)证明:∵四边形ABCD为正方形,
∴DA=DC,∠ADB=∠CDB=45°,
在△ADG和△CDG中,
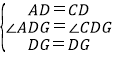 ,
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCG;
(2)解:AG⊥BE.理由如下:
∵四边形ABCD为正方形,
∴AB=DC,∠BAD=∠CDA=90°,
在△ABE和△DCF中,
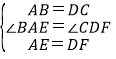 ,
,
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
∵∠DAG=∠DCG,
∴∠DAG=∠ABE,
∵∠DAG+∠BAG=90°,
∴∠ABE+∠BAG=90°,
∴∠AHB=90°,
∴AG⊥BE;
(3)解:由(2)可知AG⊥BE.
如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.
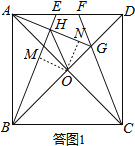
∴∠MON=90°,
又∵OA⊥OB,
∴∠AON=∠BOM.
∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,
∴∠OAN=∠OBM.
在△AON与△BOM中,
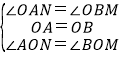 ,
,
∴△AON≌△BOM(AAS).
∴OM=ON,
∴矩形OMHN为正方形,
∴HO平分∠BHG.


科目:初中数学 来源: 题型:
【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如表所示
国外品牌 | 国内品牌 | |
进价(万元/部) | 0.44 | 0.2 |
售价(万元/部) | 0.5 | 0.25 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润
查看答案和解析>>
科目:初中数学 来源: 题型:
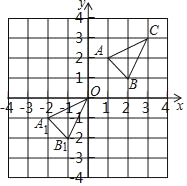
【题目】如图,已知△ABC经过平移后得到△A1B1C1,点A与A1,点B与B1,点C与C1分别是对应点,观察各对应点坐标之间的关系,解答下列问题:
(1)分别写出点A与A1,点B与B1,点C与C1的坐标;
(2)若点P(x,y)通过上述的平移规律平移得到的对应点为Q(3,5),求p点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;
(2)求证:EO=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著。书中有下列问题“今有勾八步,股十五步。问勾中容圆径几何?”其意思为今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是步。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省泰安市)某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)

根据图表提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为400人
B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中喜欢选修课E、F的人数分别为80,70
D. 喜欢选修课C的人数最少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com