
【题目】已知反比例函数y= ![]() (k≠0)的图象经过(3,﹣1),则当1<y<3时,自变量x的取值范围是 .
(k≠0)的图象经过(3,﹣1),则当1<y<3时,自变量x的取值范围是 .
【答案】﹣3<x<﹣1
【解析】解:∵反比例函数y= ![]() (k≠0)的图象经过(3,﹣1),
(k≠0)的图象经过(3,﹣1),
∴k=3×(﹣1)=﹣3,
∴反比例函数的解析式为y= ![]() .∵反比例函数y=
.∵反比例函数y= ![]() 中k=﹣3,
中k=﹣3,
∴该反比例函数的图象经过第二、四象限,且在每个象限内均单增.
当y=1时,x= ![]() =﹣3;当y=3时,x=
=﹣3;当y=3时,x= ![]() =﹣1.
=﹣1.
∴1<y<3时,自变量x的取值范围是﹣3<x<﹣1.
所以答案是:﹣3<x<﹣1.
【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1 , y1),B(x2 , y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( ) 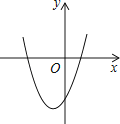
A.y1<y2
B.y1>y2
C.y的最小值是﹣3
D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
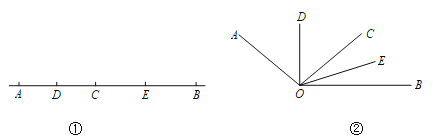
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是_____
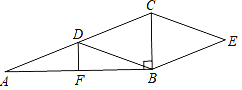
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
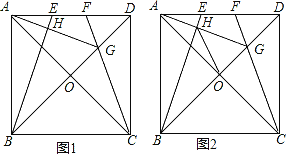
(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD内接于⊙O,如图所示,在劣弧 ![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证: 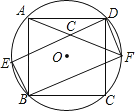
(1)四边形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个多面体的表面展开图,每个面上都标注了字母(字母在多面体的外表面),请根据要求回答问题.

(1)如果D面在多面体的左面,那么F面在哪里?
(2)B面和哪一面是相对的面?
(3)如果C面在前面,从上面看到的是D面,那么从左面能看到哪一面?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BD上有一点C,则:
(1)∠1和∠ABC是直线AB,CE被直线_____所截得的____角;
(2)∠2和∠BAC是直线CE,AB被直线____所截得的_____角;
(3)∠3和∠ABC是直线_____、_____被直线_____所截得的____角;
(4)∠ABC和∠ACD是直线____、_____被直线_____所截得的角;
(5)∠ABC和∠BCE是直线_____、______被直线所截得的_____角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,解答后面给出的问题:
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式,例如![]() 与
与![]() ,
,![]() +1与
+1与![]() -1.
-1.
(1)请你再写出两个含有二次根式的代数式,使它们互为有理化因式:__________________;
这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:![]() ,
,![]() .
.
(2)请仿照上面给出的方法化简:![]() ;
;
(3)计算:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com