
����Ŀ��2019�괺�ڣ�С�ȼҹ�����4�������������Ϸֱ�д�С����������ȡ��������������ڡ��������ȫһ������
��1��С�ȳ鵽��2019�ꡱ�������¼����������ֱ����е��������¼�����������ܡ���Ȼ�������������С�ȴ��ĸ���������ȡһ����ȡ���������ĸ�����������
��2��С�ȴ��ĸ��������Ⱥ�ȡ�����������������б�������״ͼ����С��ǡ��ȡ�������������ڡ����������ĸ��ʣ�
���𰸡���1�������ܣ������![]() ����2��
����2��![]() ��
��
��������
��1���ɲ������¼�������¼��ĸ�����ʹ�ʽ���ɵã�
��2������״ͼ�ó����еȿ��ܽ���������ҵ����������Ľ�����������ø��ʹ�ʽ����ɵã�
�⣺��1��С�ȳ鵽��2019�����Dz������¼����������ֱ����е�������¼���С�ȴ��ĸ���������ȡһ����ȡ���������ĸ�����![]() ��
��
�ʴ�Ϊ�������ܣ������![]() ��
��
��2������״ͼ���£�
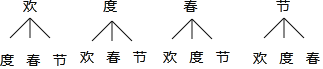
��12�ֵȿ�������������������������������е���2�֣�
���������������������еĸ����ǣ�P=![]() =
=![]() ��
��


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() ��x�ύ��A��B����A�ڵ�B����ࣩ��y�ύ�ڵ�C������AC��BC������A��AD��BC���������ڵ�D��8
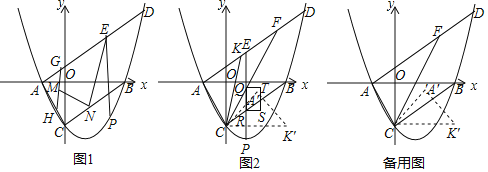
��x�ύ��A��B����A�ڵ�B����ࣩ��y�ύ�ڵ�C������AC��BC������A��AD��BC���������ڵ�D��8![]() ��10������PΪ�߶�BC�·��������ϵ�����һ�㣬����P��PE��y�ύ�߶�AD�ڵ�E��
��10������PΪ�߶�BC�·��������ϵ�����һ�㣬����P��PE��y�ύ�߶�AD�ڵ�E��
��1����ͼ1����PE+AE���ʱ���ֱ�ȡ�߶�AE��AC�϶���G��H��ʹGH=5������MΪGH���е㣬��NΪ�߶�CB��һ���㣬����EN��MN����EN+MN����Сֵ��
��2����ͼ2����F���߶�AD�ϣ���AF��DF=7��3������CF����Q��R�ֱ���PE���߶�CF��BC�Ľ��㣬��RQΪ�ߣ���RQ���Ҳ�������RQTS������RS=2������ACB�Ľ�ƽ����CK��AD�ڵ�K������ACK�Ƶ�C˳ʱ����ת75���õ���A��CK����������RQTS����A��CK���ص����֣������Ϊ0��Ϊ��Գ�ͼ��ʱ����ֱ��д����P�������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
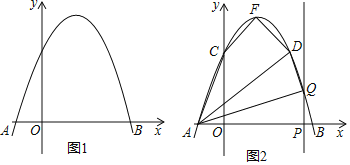
����Ŀ����ͼ1��������y=ax2+bx+3��x���ڵ�A����1��0���͵�B��3��0����
��1���������������Ӧ�ĺ�������ʽ��
��2����ͼ2������������y�ύ�ڵ�C������ΪF����D��2��3���ڸ��������ϣ�
�����ı���ACFD�������
�ڵ�P���߶�AB�ϵĶ��㣨��P�����A��B�غϣ�������P��PQ��x�ύ���������ڵ�Q������AQ��DQ������AQD��ֱ��������ʱ������������������ĵ�Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
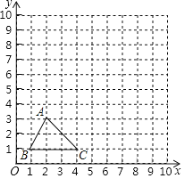
����Ŀ����ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У������˸��������![]() �����������ߵĽ���
�����������ߵĽ���![]()
![]() �Ƚ�
�Ƚ�![]() ��ֱ����ƽ��3����λ����ˮƽ����ƽ��5����λ�õ�
��ֱ����ƽ��3����λ����ˮƽ����ƽ��5����λ�õ�![]() ���뻭��
���뻭��![]() ��
��
![]() ��
��![]() ��
��![]() ��˳ʱ����ת
��˳ʱ����ת![]() ����
����![]() ���뻭��
���뻭��![]() ��
��
![]() �߶�
�߶�![]() �任��
�任��![]() �Ĺ�����ɨ����������Ϊ______��
�Ĺ�����ɨ����������Ϊ______��
![]() ����A��C����ĺ�������ʽΪ______��
����A��C����ĺ�������ʽΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Բ��ֽƬ���뾶��Ϊ1����ͼ�ص�ˮƽ���ã�����������Ͷ�����ӣ������������ص�������Ӱ���֣��ĸ��ʴ�ԼΪ��������

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
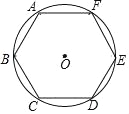
����Ŀ��κ��ʱ�ڵ���ѧ�������״���Բ����Ϊ����Բ���ʽ��������ܵ����ۺ����Ƶ��㷨����Բ�ڽ�������Σ���������εı�����������ʱ�����ܳ������ӽ�Բ���ܳ�����������![]() ����ý�Ϊ��ȷ��Բ���ʣ����֮�����յĻ����ϼ���Ŭ������������εı�������24576ʱ���õ��˾�ȷ��С�������λ��Բ���ʣ���һ�ɾ��ڵ�ʱ��������������һǧ���꣬��ͼ����������Բ��������Բ�ڽ�����������õ�Բ���ʵĽ���ֵ��( )
����ý�Ϊ��ȷ��Բ���ʣ����֮�����յĻ����ϼ���Ŭ������������εı�������24576ʱ���õ��˾�ȷ��С�������λ��Բ���ʣ���һ�ɾ��ڵ�ʱ��������������һǧ���꣬��ͼ����������Բ��������Բ�ڽ�����������õ�Բ���ʵĽ���ֵ��( )
A. 0.5B. 1C. 3D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����![]() ������AC������C��ֱ��l��AB����P��ֱ��l�ϵ�һ�����㣬ֱ��PA���O������һ��D������CD����ֱ��PB��ֱ��AC���ڵ�E��
������AC������C��ֱ��l��AB����P��ֱ��l�ϵ�һ�����㣬ֱ��PA���O������һ��D������CD����ֱ��PB��ֱ��AC���ڵ�E��
��1�����BAC�Ķ�����
��2������D��AB�Ϸ�����CD��BPʱ����֤��PC=AC��
��3���ڵ�P���˶�������
�ٵ���A���߶�PB���д����ϻ��B���߶�PA���д�����ʱ������������������ġ�ACD�Ķ�����
�����O�İ뾶Ϊ6����E��ֱ��l�ľ���Ϊ3������BD��DE��ֱ��д����BDE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����ֲ�ͬ�ͺŵ��·�����֪����A���ͺ��·�9����B���ͺ��·�10��������1810Ԫ��������A���ͺ��·�12����B���ͺ��·�8��������1880Ԫ����֪����һ��A�ͺ��·��ɻ���18Ԫ������һ��B�ͺ��·��ɻ���30Ԫ��Ҫʹ����������л���������699Ԫ����A�ͺ��·�������28����
��1����A��B�ͺ��·����۸��Ƕ���Ԫ��
��2������֪����A�ͺ��·���B�ͺ��·���2������4�������̵�����ν����п��м��ַ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��50Ԫ�����ۼ�Ϊÿ��70Ԫʱ��ÿ���ڿ�����300�������轵�۴������Ҿ��г����飺ÿ����1Ԫ��ÿ���ڿɶ�����20������ȷ��ӯ����ǰ���£�����������⣺
��1������ÿ������xԪ��ÿ�����۳���Ʒ������ΪyԪ����д��y��x�ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�������۶���Ԫʱ��ÿ���ڵ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com