
【题目】阅读下面材料,并解决问题:问 题:如图1,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为6,8,10,求∠APB的度数?


分 析:由于PA,PB,PC不在同一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′和△ABP全等,这样,就可以利用全等三角形知识,将三条线段的长度转化到同一个三角形中从而求出∠APB的度数.
(1)请你按上述方法求出图1中∠APB的度数;
(2)请你利用第(1)题的解答思想方法,解答下面问题:如图2,已知△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°,求证:EF2=BE2+FC2 .
【答案】(1)150°;(2)证明见解析.
【解析】试题分析:(1)根据旋转变换前后的两个三角形全等,全等三角形对应边相等,全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理解答;
(2)把△ABE绕点A逆时针旋转90°得到△ACE′,根据旋转的性质可得AE′=AE,CE′=CE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,再求出∠E′AF=45°,从而得到∠EAF=∠E′AF,然后利用“边角边”证明△EAF和△E′AF全等,根据全等三角形对应边相等可得E′F=EF,再利用勾股定理列式即可得证.
试题解析:解:(1)∵△ACP′≌△ABP, ∴AP′=AP=3、CP′=BP=4、∠AP′C=∠APB,.
由题意知旋转角∠PA P′=60°,∴△AP P′为等边三角形,P P′=AP=3,∠A P′P=60°,易证△P P′C为直角三角形,且∠P P′C=90°,∴∠APB=∠AP′C=∠A P′P+∠P P′C=60°+90°=150°
(2)把△ABE绕点A逆时针旋转90°得到△ACE′,由旋转的性质得,AE′=AE,CE′=CE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,∵∠EAF=45°,∴∠E′AF=∠CAE′+∠CAF=∠BAE+∠CAF=∠BAC﹣∠EAF=90°﹣45°=45°,∴∠EAF=∠E′AF,在△EAF和△E′AF中,∵AE=AE′,∠EAF=∠E′AF,AF=AF,∴△EAF≌△E′AF(SAS),∴E′F=EF,∵∠CAB=90°,AB=AC,∴∠B=∠ACB=45°,∴∠E′CF=45°+45°=90°,由勾股定理得,E′F2=CE′2+FC2 ,即EF2=BE2+FC2 .



科目:初中数学 来源: 题型:
【题目】如图表示某市2016年6月份某一天的气温随时间变化的情况,请观察此图回答下列问题:
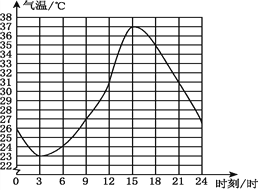
(1)这天的最高气温是多少摄氏度?
(2)这天共有多少个小时的气温在31 ℃以上?
(3)这天什么时间范围内气温在上升?
(4)请你预测一下,次日凌晨1时的气温大约是多少摄氏度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 与正比例函数y2=k2x相交于点A(-1,-3)和点B.
与正比例函数y2=k2x相交于点A(-1,-3)和点B.
(1)求k1,k2的值;
(2)写出点B的坐标;
(3)写出![]() >k2x的解集.
>k2x的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是张阳离家的距离与时间的关系图象.
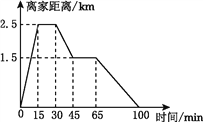
根据图象回答下列问题:
(1)体育场离张阳家多少千米?
(2)体育场离文具店多少千米?张阳在文具店逗留了多长时间?
(3)张阳从文具店到家的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【课本引申】
我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
【尝试探究】
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?

【拓展运用】
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=_________;

(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案_ .

(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的重量(kg)之间的关系如下表:
所挂物体的重量(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 |
(1)当所挂物体的重量为3kg时,弹簧的长度是_____________cm;
(2)如果所挂物体的重量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(3)当所挂物体的重量为5.5kg时,请求出弹簧的长度。
(4)如果弹簧的最大伸长长度为20cm,则该弹簧最多能挂多重的物体?
查看答案和解析>>
科目:初中数学 来源: 题型:
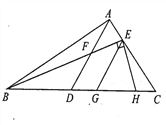
【题目】如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H,∠HEG = 50°.
(1)求∠BFD的度数.
(2)若∠BAD = ∠EBC,∠C = 41°,求∠BAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com