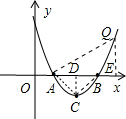
解:(1)∵顶点坐标为C(4,-

),且与x轴的两个交点间的距离为6,
∴对称轴x=4,A(1,0),B(7,0),
设抛物线解析式y=a(x-1)(x-7),将C点坐标代入可得a=

,
∴所求解析式为y=

x
2-

x+
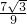
;
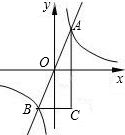
(2)在x轴上方的抛物线上存在点Q,使得以点Q、A、B为顶点的三角形与△ABC相似,
因为△ABC为等腰三角形,
∴当AB=BQ,
∵AB=6,
∴BQ=6,过点C作CD⊥x轴于D,则AD=3,CD=

∴∠BAC=∠ABC=30°,
∴∠ACB=120°,
∴∠ABQ=120°,过点Q作QE⊥x轴于E,则∠QBE=60°,
∴QE=BQsin60°=6×

=3

,
∴BE=3,
∴E(10,0),
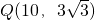
.
当x=10时,y=

×10
2-

×10+
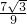
=3

;
∴点Q在抛物线上,由抛物线的对称性,
还存在一点
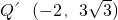
,使△ABQ′∽△CAB故存在点
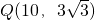
或
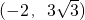
.
分析:(1)已知顶点,就已知对称轴,又AB=6,可求A、B两点坐标了,可设抛物线交点式求解;
(2)根据点的坐标先研究△ABC的特殊性,AC=BC,∠A=∠B=30°,故△ABQ也是等腰三角形,AB为腰,且∠A=30°或者∠B=30°,通过解直角三角形可求Q点坐标,再判断Q点是否在抛物线上.
点评:本题考查了点的坐标及抛物线解析式的求法,在抛物线上寻找三角形相似的条件的方法.

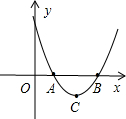 在直角坐标系XOY中,二次函数图象的顶点坐标为
在直角坐标系XOY中,二次函数图象的顶点坐标为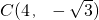 ,且与x轴的两个交点间的距离为6.
,且与x轴的两个交点间的距离为6. 解:(1)∵顶点坐标为C(4,-
解:(1)∵顶点坐标为C(4,- ),且与x轴的两个交点间的距离为6,
),且与x轴的两个交点间的距离为6, ,
, x2-
x2- x+
x+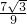 ;
;
 =3
=3 ,
,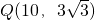 .
. ×102-
×102- ×10+
×10+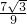 =3
=3 ;
;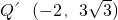 ,使△ABQ′∽△CAB故存在点
,使△ABQ′∽△CAB故存在点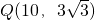 或
或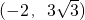 .
.


 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.