
【题目】如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD. 
(1)若∠DOF=25°,求∠AOB的度数.
(2)若OA平分∠BOE,则∠DOF的度数是 . (直接写出答案)
【答案】
(1)解:∵∠DOF=25°,OF平分∠COD,
∴∠DOC=50°,
∵OB⊥OD,
∴∠BOC=90°﹣50°=40°,
∵OA⊥OC,
∴∠AOB=90°﹣∠BOC=50°
(2)30°
【解析】解:(2)∵∠BOC+∠COD=90°,∠AOB+∠BOC=90°,
∴∠COD=∠AOB,
设∠DOF=∠COF=x,
∵OA平分∠BOE,
∴∠AOE=∠AOB=∠COD=2x,∠BOC=90°﹣2x,
∴5x+90°﹣2x=180°,
解得:x=30°,
即∠DOF=30°.
故答案为:30°.
(1)利用角平分线的定义可得∠DOC=50°,由垂直的定义可得∠BOD=90°,易得∠BOC=40°,因为OA⊥OC,可得结果;(2)利用垂直的定义易得∠BOC+∠COD=90°,∠AOB+∠BOC=90°,可得∠COD=∠AOB,设∠DOF=∠COF=x,利用平分线的定义可得∠AOE=∠AOB=∠COD=2x,∠BOC=90°﹣2x,由平角的定义可得5x+90°﹣2x=180°,解得x,即得结果.


科目:初中数学 来源: 题型:
【题目】表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x与方差s2,根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
甲 | 乙 | 丙 | 丁 | |
平均数x/cm | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD平分∠BAC;②作图依据是S.A.S;③∠ADC=60°; ④点D在AB的垂直平分线上
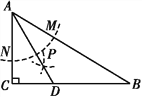
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A. 众数 B. 方差 C. 平均数 D. 中位数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com