【题目】表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x与方差s2，根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择( )
甲 | 乙 | 丙 | 丁 | |
平均数x/cm | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
A.甲B.乙C.丙D.丁
科目：初中数学 来源： 题型：
【题目】观察下列关于x的单项式，探究其规律：
x，3x2 ， 5x3 ， 7x4 ， 9x5 ， 11x6 ， …
按照上述规律，第2015个单项式是（ ）
A.2015x2015
B.4029x2014
C.4029x2015
D.4031x2015
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】疫情期间，某地向武汉捐赠口罩1200000只，其中数1200000用科学记数法表示是（ ）
A.12×105B.12×106C.1.2×105D.1.2×106
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若△ABC的每条边长增加各自的10%得△A′B′C′，则∠B′的度数与其对应角∠B的度数相比（ ）
A.增加了10%
B.减少了10%
C.增加了（1+10%）
D.没有改变
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点O是直线EF上一点，射线OA，OB，OC在直线EF的上方，射线OD的直线EF的下方，且OF平分∠COD，OA⊥OC，OB⊥OD． 
（1）若∠DOF=25°，求∠AOB的度数．
（2）若OA平分∠BOE，则∠DOF的度数是 ． （直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
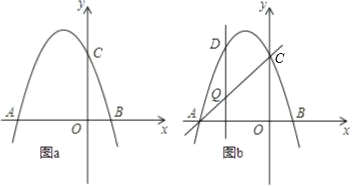
【题目】如图，抛物线y=﹣x2+bx+c交x轴于点A（﹣3，0）和点B，交y轴于点C（0，3）．
（1）求抛物线的函数表达式；
（2）若点P在抛物线上，且S△AOP=4SBOC，求点P的坐标；
（3）如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(10分)如图①，将两块全等的三角板拼在一起，其中△ABC的边BC在直线l上，AC⊥BC且AC = BC；△EFP的边FP也在直线l上，边EF与边AC重合，EF⊥FP且EF = FP。
（1）在图①中，请你通过观察、测量，猜想并写出AB与AP所满足的数量关系和位置关系；
（2）将三角板△EFP沿直线l向左平移到图②的位置时，EP交AC于点Q，连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系，并证明你的猜想；
（3）将三角板△EFP沿直线l向左平移到图③的位置时，EP的延长线交AC的延长线于点Q，连接AP、BQ。你认为（2）中猜想的BQ与AP所满足的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
