
����Ŀ����֪����ͼ�٣����ı���ABCD�У�AB��CD����B��90�㣬��P��BC���ϣ�����APD��90��ʱ����֪��ABP�ס�PCD������Ҫ��֤����
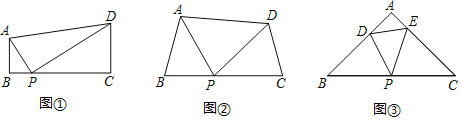
̽������ͼ�ڣ����ı���ABCD�У���P��BC���ϣ�����B����C����APDʱ����֤����ABP�ס�PCD��
��չ����ͼ�ۣ��ڡ�ABC�У���P�DZ�BC���е㣬��D��E�ֱ��ڱ�AB��AC�ϣ�����B����C����DPE��45�㣬BC��6![]() ��BD��4����DE�ij�Ϊ�� ����
��BD��4����DE�ij��� ����
���𰸡�̽��������������չ��![]() .
.
��������
��֪�����жϳ���BAP����DPC�������ó����ۣ�
̽��������������ȣ������������ƣ������ó����ۣ�
��չ��������BDP�ס�CPE�ó�����ʽ���CE������������ڽǺͶ���֤��AC��AB��AC��AB�������ֱ����ADE�����ù��ɶ�������DE�ij��ȣ�
�⣺��֪���ߡ�APD��90����
���APB+��DPC��90����
�ߡ�B��90����
���APB+��BAP��90����
���BAP����DPC��
��AB��CD����B��90����
���C����B��90����
���ABP�ס�PCD��
̽�����ߡ�APC����BAP+��B����APC����APD+��CPD��
���BAP+��B����APD+��CPD��
�ߡ�B����APD��
���BAP����CPD��
�ߡ�B����C��
���ABP�ס�PCD��
��չ��ͬ̽���ķ����ó�����BDP�ס�CPE��
��![]() ��
��
�ߵ�P�DZ�BC���е㣬
��BP��CP��3![]() ��
��
��BD��4��
��![]() ��
��
��CE��![]() ��
��
�ߡ�B����C��45����
���A��180������B����C��90����
��AC��AB��AC��AB��6��
��AE��AC��CE��6��![]() ��
��![]() ��AD��AB��BD��6��4��2��
��AD��AB��BD��6��4��2��
��Rt��ADE��DE��![]() ��
�� ��
��![]() ��
��
�ʴ��ǣ�![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������![]() ������˵������ȷ���ǣ�������
������˵������ȷ���ǣ�������
A. ����ͼ��ֱ�λ�ڵ�һ����������
B. ��x��0ʱ��y��x���������С
C. ����A��x1��y1����B��x2��y2�����ں���ͼ���ϣ���x1��x2����y1��y2
D. ����ͼ���㣨1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
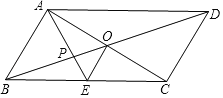
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AEƽ�֡�BAD���ֱ�BC��BD�ڵ�E��P������OE����ADC=60�㣬AB=![]() BC=1�������н��ۣ�
BC=1�������н��ۣ�
�١�CAD=30����BD=![]() ��Sƽ���ı���ABCD=ABAC��OE=
��Sƽ���ı���ABCD=ABAC��OE=![]() AD��S��APO=
AD��S��APO=![]() ����ȷ�ĸ����ǣ�������
����ȷ�ĸ����ǣ�������
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
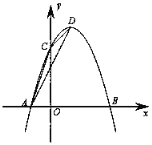
����Ŀ����ͼ��������y��ax2+bx+3��x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣬�ֱ�����AC��CD��AD��
��1���������ߵĺ�������ʽ�Լ�����D�����ꣻ
��2������������ȡһ��P�������C�غϣ������ֱ�����PA��PD������PAD���������ACD��������ʱ�����P�����ꣻ
��3������1��������õ���������A��D���ڵ�ֱ��ƽ�ƣ�ƽ�ƺ��A�Ķ�Ӧ��ΪA������C�Ķ�Ӧ��ΪC������D�Ķ�Ӧ��ΪD�������ı���AA��C��C������ʱ�����ʱƽ�ƺ�������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ����������⣺
��1���ٷ���x2-x-2 =0�Ľ�Ϊ__________
�ڷ���x2-2x-3 =0�Ľ�Ϊ_______
�۷���x2-3x-4 =0�Ľ�Ϊ_______
...
��2���������Ϸ�����������������������룺
�ٷ���x2-9x-10=0�Ľ�Ϊ_______
�������䷽���ⷽ��x2-9x-10=0,����֤������۵���ȷ�ԡ�
��3��Ӧ�ã�����x�ķ���______�Ľ�Ϊx1 =-1,x2 =n+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() ���������ཻ���䶥������Ϊ
���������ཻ���䶥������Ϊ![]() �����н��ۣ���
�����н��ۣ���![]() ����
����![]() ����
����![]() ��������
��������![]() ��������ȵ�ʵ������������ȷ�Ľ�����________����ֻ����ż��ɣ���
��������ȵ�ʵ������������ȷ�Ľ�����________����ֻ����ż��ɣ���
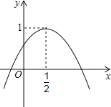
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ�ǡ�ABC����������ֱ���A����3��1����B��0��3����C��0��1��

��1������ABC�Ե�CΪ��ת������ת180�㣬������ת���Ӧ�ġ�A1B1C1��
��2���ֱ�����AB1��BA1�����ı���AB1A1B�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ڵ�λ����Ϊ1�������������У�һ��Բ����������Ľ���A��B��C��
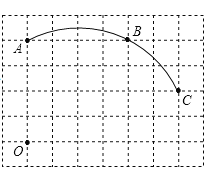
��1����������²�����
���Ե�OΪ����ԭ�㡢��ֱ��ˮƽ����Ϊ�ᡢ����߳�Ϊ��λ��������ƽ��ֱ������ϵ�����ڸ���ͼ���ṩ����Ϣ�������Բ������Բ��Բ��D��������AD��CD��
��2�����ڣ�1���Ļ����ϣ����������գ�
��д��������꣺C ��D ��
�ڡ�D�İ뾶= ������������ţ���
����E��7��0�������ж�ֱ��EC���D��λ�ù�ϵ����˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
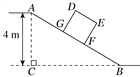
����Ŀ����ͼ��ij�ִ�������һб��AB�����±�Ϊi��1��2������A���ĸ�ACΪ4 m��B��C��ͬһˮƽ���ϣ�
(1)��б��AB��ˮƽ����BC��
(2)����DEFGΪ�����λ���IJ���ͼ������DE��2.5 m��EF��2 m����������б���������ͣ���BF��3.5 mʱ�����D�����ĸߣ�(![]() ��2.236�������ȷ��0.1 m)
��2.236�������ȷ��0.1 m)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com