
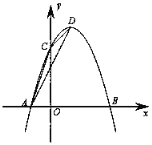
����Ŀ����ͼ��������y��ax2+bx+3��x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣬�ֱ�����AC��CD��AD��
��1���������ߵĺ�������ʽ�Լ�����D�����ꣻ
��2������������ȡһ��P�������C�غϣ������ֱ�����PA��PD������PAD���������ACD��������ʱ�����P�����ꣻ
��3������1��������õ���������A��D���ڵ�ֱ��ƽ�ƣ�ƽ�ƺ��A�Ķ�Ӧ��ΪA������C�Ķ�Ӧ��ΪC������D�Ķ�Ӧ��ΪD�������ı���AA��C��C������ʱ�����ʱƽ�ƺ�������ߵĽ���ʽ��
���𰸡���1��y����x2+2x+3����1��4������2��![]() ��
��![]() ����3���ٵ�A����x���Ϸ�ʱ����ͼ2��A��������Ϊ��
����3���ٵ�A����x���Ϸ�ʱ����ͼ2��A��������Ϊ��![]() ��1��2
��1��2![]() �����ڵ�A����x���·�ʱ����ͼ3��ͬ���ɵã�ƽ�ƺ��������Ϊy��
�����ڵ�A����x���·�ʱ����ͼ3��ͬ���ɵã�ƽ�ƺ��������Ϊy��![]()
��������
��1�����C�����꣬Ȼ�����A��B��������������ߵĺ�������ʽΪy��a��x+1����x��3��������c�����꼴�����a����ý���ʽ��������ö������ꣻ
��2�������ֱ��AD�Ľ���ʽ��Ȼ������߶�AD��y���ڵ�E������꣬����C��ֱ��l1��AD����ֱ��l1�Ľ���ʽΪy��2x+3������������ߵĽ���C����C�����꼴���ж����߶�AD�Ϸ����������ϲ�����ʹ��PAD���������ACD�������ȵĵ�P����ֱ��AD����ֱ��������ƽ��1����λ���ȣ����õ�ֱ��l2�Ľ���ʽΪy��2x+1��ֱ��l2�������߽��ڵ�P�����ʱ��PAD���������ACD�������ȣ��������̼�����ý���P�����ꣻ
��3����A��������Ϊ��t��2t+2������ó�A��A2��5��t+1��2��AC2��10�����ı���AA��C��C�����Σ���AC��AA�����Ӷ��ó�5��t+1��2��10�����t1��![]() ��1��t2����
��1��t2����![]() ��1���������A����������
��1���������A����������![]() ��1��2
��1��2![]() ����
����![]() ��1����2
��1����2![]() ����Ȼ����������������ü��ɣ�
����Ȼ����������������ü��ɣ�
�⣺��1����������y��ax2+bx+3��֪C������Ϊ��0��3����
�������ߵĺ�������ʽΪy��a��x+1����x��3����
����C��0��3���é�3a��3��
��a����1��
�������ߵĺ�������ʽΪy������x+1����x��3������y����x2+2x+3��
�߶Գ���Ϊֱ��x��![]() ��1��
��1��
������ʽ����y������1+1����1��3����4��
�ඥ��D������Ϊ��1��4����
��2����C��0��3����OC��3��
��ֱ��AD�Ľ���ʽΪy��kx+m����
![]() �����
�����![]()
��ֱ��AD�Ľ���ʽΪy��2x+2��
���߶�AD��y���ڵ�E����E��0��2����
��CE��OC��OE��3��2��1��
����C��ֱ��l1��AD����ֱ��l1�Ľ���ʽΪy��2x+3����ͼ1��
�ɩ�x2+2x+3��2x+3�����x1��x2��0��
��x��0����y��2x+3����y��3��
��ֱ��l1��������ֻ��һ������C��
�����߶�AD�Ϸ����������ϲ�����ʹ��PAD���������ACD�������ȵĵ�P��
��ֱ��AD����ֱ��������ƽ��1����λ���ȣ����õ�ֱ��l2�Ľ���ʽΪy��2x+1��
ֱ��l2�������߽��ڵ�P�����ʱ��PAD���������ACD�������ȣ�
�ɩ�x2+2x+3��2x+1�����x1��![]() ��x2����
��x2����![]() ��
��
��y1��2![]() +1��y2����2
+1��y2����2![]() +1��
+1��
���P��������![]() ��2
��2![]() +1����
+1����![]() ����2
����2![]() +1����
+1����
��3����A����������t��2t+2����
��A��A2����t+1��2+��2t+2��2��5��t+1��2��AC2��12+32��10��
���ı���AA��C��C�����Σ�
��AC��AA����
��5��t+1��2��10�����t1��![]() ��1��t2����
��1��t2����![]() ��1��
��1��
��A����������![]() ��1��2
��1��2![]() ����
����![]() ��1����2
��1����2![]() ����
����
�ٵ�A����x���Ϸ�ʱ����ͼ2��A��������Ϊ��![]() ��1��2
��1��2![]() ����
����
����A������ƽ��![]() ����λ���ȣ�������ƽ��2
����λ���ȣ�������ƽ��2![]() ����λ���Ⱦ͵õ���A����
����λ���Ⱦ͵õ���A����
�ཫ��D��1��4��������ƽ��![]() ����λ���ȣ�������ƽ��2
����λ���ȣ�������ƽ��2![]() ����λ���Ⱦ͵õ���D����
����λ���Ⱦ͵õ���D����![]() +1��2
+1��2![]() +4����
+4����
��ƽ�ƺ��������Ϊy������x��![]() ��1�� 2+4+2
��1�� 2+4+2![]() ��
��
�ڵ�A����x���·�ʱ����ͼ3��ͬ���ɵã�ƽ�ƺ��������Ϊy������x��1+![]() �� 2+4��2
�� 2+4��2![]() ��
��






| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����α߳�Ϊ1�������У���A��B��C���ڸ���ϣ�
����AC�ij��ȵ���_____��
��������ͼ����һ��P��������AP��PB��PC������APƽ�֡�A����PC=PB��������ͼ��ʾ�������У����̶ȵ�ֱ�ߣ�������P������Ҫ˵����P��λ��������ҵ��ģ���Ҫ��֤����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����һ����Ʒ��ÿ���ɱ�Ϊ20Ԫ�����г����鷢�֣���һ��ʱ���ڣ�������w�����������۵���x��Ԫ/�����ı仯���仯�������ϵʽΪ��w=-10x+500����������Ʒ�����ʱ���ڵ���������Ϊy��Ԫ��������������⣺
��1����y��x�ĺ�����ϵʽ��
��2����xȡ��ֵʱ����������������Ϊ����Ԫ��
��3�������۲��Ź涨������Ʒ�����۵��۲��ø���32Ԫ/������˾��Ҫ�����ʱ���ڻ��2000Ԫ�������������۵���Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��k1x+b�뷴��������![]() ��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪��A�������ǣ�6��2����B���������ǩ�3��
��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪��A�������ǣ�6��2����B���������ǩ�3��

��1������������ֱ��l1�ı���ʽ��
��2������ͼ��ֱ��д��k1x+b��![]() �Ľ⼯��
�Ľ⼯��
��3����ֱ��l1��![]() ��y������ƽ�ƺ��ֱ��l2�뷴��������
��y������ƽ�ƺ��ֱ��l2�뷴��������![]() �ڵ�һ�����ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
�ڵ�һ�����ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
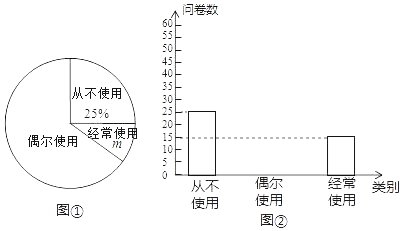
����Ŀ������̼�����ɫ�����������dz�����һ�����ʽ��ijУΪ�˽�ѧ���Թ���������ʹ������������ȡ����ѧ�������ʾ����飬������ε���Ľ������������������������ͳ��ͼ��
����������Ϣ������������⣺
��1��m���� ����
��2����ȫ����ͳ��ͼ��
��3������������������ ����
��4����֪ȫУ��3000��ѧ���������������ʹ��������������ѧ����Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ϊ������������ȥ��ˮ��羰�����Σ��Ƴ��������շѱ���
 ij��λ��֯Ա��ȥ��ˮ��羰�����Σ���֧�����������������η���27000Ԫ�����ʸõ�λ��ι��ж���Ա��ȥ��ˮ��羰�����Σ�
ij��λ��֯Ա��ȥ��ˮ��羰�����Σ���֧�����������������η���27000Ԫ�����ʸõ�λ��ι��ж���Ա��ȥ��ˮ��羰�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�٣����ı���ABCD�У�AB��CD����B��90�㣬��P��BC���ϣ�����APD��90��ʱ����֪��ABP�ס�PCD������Ҫ��֤����
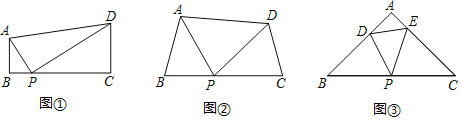
̽������ͼ�ڣ����ı���ABCD�У���P��BC���ϣ�����B����C����APDʱ����֤����ABP�ס�PCD��
��չ����ͼ�ۣ��ڡ�ABC�У���P�DZ�BC���е㣬��D��E�ֱ��ڱ�AB��AC�ϣ�����B����C����DPE��45�㣬BC��6![]() ��BD��4����DE�ij�Ϊ�� ����
��BD��4����DE�ij��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����Ը��Ϊ����������γ�Ϊ��������Σ�ÿ��С�����DZ߳�Ϊ1�������Σ���ͼ����ABC�Ǹ�������Σ���A��B��C������ֱ��ǣ���4����1��������2����3��������1����2����
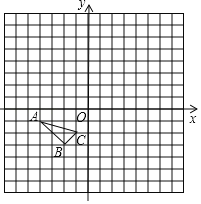
��1����OΪ��ת���ģ�����ABC��O��˳ʱ����ת90����õ���A1B1C1��������A1B1C1��
��2����OΪλ�����ģ��ڵ�һ�����ڰ���ABC�Ŵ�2����õ���A2B2C2��������A2B2C2��
��3����ABC����һ��P��a��b����д��������2��λ�Ʊ任��P�Ķ�Ӧ��P1�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���߲˵����۵���y1�������·�x֮��Ĺ�ϵ��ͼ��1����ʾ���ɱ�y2�������·�֮��Ĺ�ϵ��ͼ��2����ʾ��ͼ��1����ͼ�����߶�ͼ��2����ͼ���������ߣ�
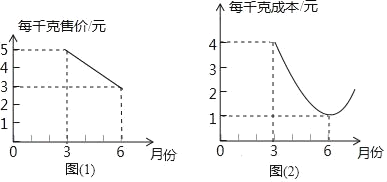
��1���ֱ����y1��y2�ĺ�����ϵʽ����д�Ա���ȡֵ��Χ����
��2��ͨ������˵�����ĸ��³��������߲ˣ�ÿǧ�˵��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com