
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����Ը��Ϊ����������γ�Ϊ��������Σ�ÿ��С�����DZ߳�Ϊ1�������Σ���ͼ����ABC�Ǹ�������Σ���A��B��C������ֱ��ǣ���4����1��������2����3��������1����2����
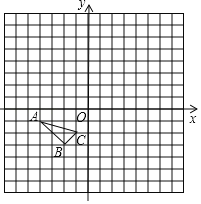
��1����OΪ��ת���ģ�����ABC��O��˳ʱ����ת90����õ���A1B1C1��������A1B1C1��
��2����OΪλ�����ģ��ڵ�һ�����ڰ���ABC�Ŵ�2����õ���A2B2C2��������A2B2C2��
��3����ABC����һ��P��a��b����д��������2��λ�Ʊ任��P�Ķ�Ӧ��P1�����꣮
���𰸡���1����ͼ����A1B1C1Ϊ����������������2����ͼ����A2B2C2Ϊ����������������3����P�Ķ�Ӧ��P1������Ϊ����2a����2b����
��������
��1�����������ص����ת����������������A��B��C�Ķ�Ӧ��A1��B1��C1�����꣬��˳�����Ӽ��ɣ�
��2���ѵ�A��B��C�ĺ������궼���ԣ�2�õ���A2��B2��C2�����꣬��˳�����Ӽ��ɣ�
��3�����ݣ�2�����Ӧ��������ص����.
��1����ͼ����A1B1C1Ϊ������
��2����ͼ����A2B2C2Ϊ������

��3����P�Ķ�Ӧ��P1������Ϊ����2a����2b����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ǡ�ABC�У�AB=5��tanC=3��BD��AC�ڵ�D��BD=3����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���AB���յ�B�˶�������P��PE��AC����BC�ڵ�E����PEΪ����Rt��PEF��ʹ��EPF=90������F�ڵ�P���·�����EF��AB�����PEF���ABD�ص�����ͼ�ε����ΪS��ƽ����λ����S��0������P���˶�ʱ��Ϊt���룩��t��0����
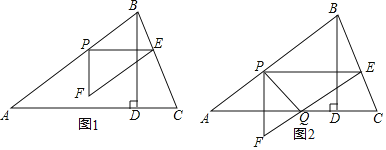
��1��ֱ��д���߶�AC�ij�Ϊ ��
��2������PEF���ABD�ص�����ͼ��Ϊ�ı���ʱ����S��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3������EF����ֱ�����AC���ڵ�Q������PQ����ͼ2��
�ٵ�PQ����PEF������ֳ�1:2������ʱ����AP�ij���
��ֱ��д����ABC��ijһ���㵽P��Q����������ʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
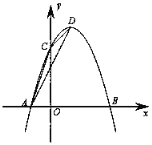
����Ŀ����ͼ��������y��ax2+bx+3��x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣬�ֱ�����AC��CD��AD��
��1���������ߵĺ�������ʽ�Լ�����D�����ꣻ
��2������������ȡһ��P�������C�غϣ������ֱ�����PA��PD������PAD���������ACD��������ʱ�����P�����ꣻ
��3������1��������õ���������A��D���ڵ�ֱ��ƽ�ƣ�ƽ�ƺ��A�Ķ�Ӧ��ΪA������C�Ķ�Ӧ��ΪC������D�Ķ�Ӧ��ΪD�������ı���AA��C��C������ʱ�����ʱƽ�ƺ�������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() ���������ཻ���䶥������Ϊ
���������ཻ���䶥������Ϊ![]() �����н��ۣ���
�����н��ۣ���![]() ����
����![]() ����
����![]() ��������
��������![]() ��������ȵ�ʵ������������ȷ�Ľ�����________����ֻ����ż��ɣ���
��������ȵ�ʵ������������ȷ�Ľ�����________����ֻ����ż��ɣ���
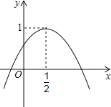
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ�ǡ�ABC����������ֱ���A����3��1����B��0��3����C��0��1��

��1������ABC�Ե�CΪ��ת������ת180�㣬������ת���Ӧ�ġ�A1B1C1��
��2���ֱ�����AB1��BA1�����ı���AB1A1B�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�濿ǽ�Ŀյ����ó�24m����ʣ�Χ���м����������ʵij����λ��ԣ��軨�Ե�һ��ABΪx��m�������S��m2����

��1����S��x֮��ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��2����ǽ�������ó���Ϊ8m����Χ�ɻ��Ե���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ڵ�λ����Ϊ1�������������У�һ��Բ����������Ľ���A��B��C��
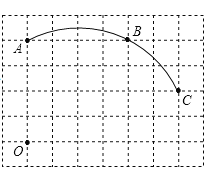
��1����������²�����
���Ե�OΪ����ԭ�㡢��ֱ��ˮƽ����Ϊ�ᡢ����߳�Ϊ��λ��������ƽ��ֱ������ϵ�����ڸ���ͼ���ṩ����Ϣ�������Բ������Բ��Բ��D��������AD��CD��
��2�����ڣ�1���Ļ����ϣ����������գ�
��д��������꣺C ��D ��
�ڡ�D�İ뾶= ������������ţ���
����E��7��0�������ж�ֱ��EC���D��λ�ù�ϵ����˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺 ![]()
��2����֪����ͼ���ڡ�ABC�У�AB��AC����D��E��F�ֱ��ǡ�ABC���ߵ��е㣬��֤���ı���AEDF�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��
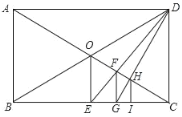
��1������O��OE��BC�ڵ�E������DE��OC�ڵ�F����FG��BC��G�㣬����ABC����FGC��λ��ͼ�������ǣ���˵��λ�����ģ������λ�Ʊȣ������ǣ���˵�����ɣ�
��2������DG��AC�ڵ�H����HI��BC��I����ȷ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com