
【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O.
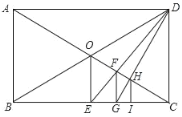
(1)过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出位似比;若不是,请说明理由.
(2)连接DG交AC于点H,作HI⊥BC于I,试确定![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形).图中△ABC是格点三角形,点A,B,C的坐标分别是(﹣4,﹣1),(﹣2,﹣3),(﹣1,﹣2).
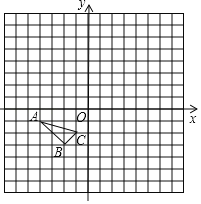
(1)以O为旋转中心,把△ABC绕O点顺时针旋转90°后得到△A1B1C1,画出△A1B1C1;
(2)以O为位似中心,在第一象限内把△ABC放大2倍后得到△A2B2C2,画出△A2B2C2;
(3)△ABC内有一点P(a,b),写出经过(2)位似变换后P的对应点P1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)
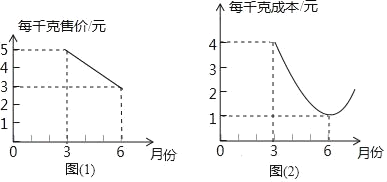
(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
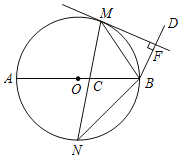
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
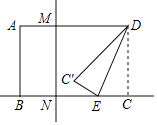
【题目】如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=![]() AD,BN=
AD,BN=![]() BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品的进价为每件30元,销售过程中发现月销售量y(件)与销售单价x(元)之间的关系如图所示.
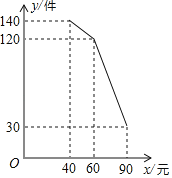
(1)根据图象直接写出y与x之间的函数关系式.
(2)设这种商品月利润为W(元),求W与x之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠BAD=120°,点E在射线AC上(不包括点A和点C),过点E的直线GH交直线AD于点G,交直线BC于点H,且GH∥DC,点F在BC的延长线上,CF=AG,连接ED,EF,DF.
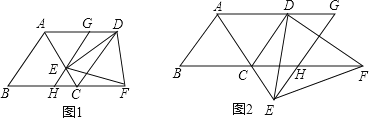
(1)如图1,当点E在线段AC上时,
①判断△AEG的形状,并说明理由.
②求证:△DEF是等边三角形.
(2)如图2,当点E在AC的延长线上时,△DEF是等边三角形吗?如果是,请证明你的结论;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com