
【题目】已知二次函数![]() 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:①![]() ;②
;②![]() ; ③abc>0;④4a-2b+c<0;⑤c-a>1其中所有正确结论的序号是______
; ③abc>0;④4a-2b+c<0;⑤c-a>1其中所有正确结论的序号是______

【答案】①②③⑤
【解析】
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线当x=1、x=-1和x=-2时的情况进行推理,进而对所得结论进行判断.
①当x=1时,y=a+b+c<0,故①正确;
②当x=1时,y=ab+c>1,故②正确;
③由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上,
∴c>0,对称轴为![]() ,得2a=b,
,得2a=b,
∴a、b同号,即b<0,
∴abc>0,故③正确;
④∵对称轴为![]() ,
,
∴点(0,1)的对称点为(2,1),
∴当x=2时,y=4a2b+c=1>0,故④错误;
⑤∵x=1时,ab+c>1,又对称轴为![]() ,即b=2a,
,即b=2a,
∴ca>1,故⑤正确.
故答案为:①②③⑤.


科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)+40+(﹣32)+(﹣8)
(2)12﹣(﹣18)+(﹣7)
(3)(+3![]() )﹣(﹣5
)﹣(﹣5![]() )+(﹣2
)+(﹣2![]() )﹣(﹣32
)﹣(﹣32![]() )
)
(4)81.26﹣293.8+8.74+111
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=2x+4交x轴于A,交y轴于B.

(1) 直接写出直线l向右平移2个单位得到的直线l1的解析式_______;
(2) 直接写出直线l关于y=-x对称的直线l2的解析式_______;
(3) 点P在直线l上,若S△OAP=2S△OBP,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为2的等边三角形ABC的顶点C作直线l⊥ BC,然后作△ABC关于直线l对称的△A′B′C,P为线段A′C上一动点,连接AP,PB,则AP+PB的最小值是 ( )
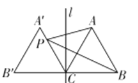
A.4B.3C.2D.2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
“若x满足(210﹣x)(x﹣200)=﹣204,试求(210﹣x)2+(x﹣200)2的值”.
解:设210﹣x=a,x﹣200=b,则ab=﹣204,且a+b=210﹣x+x﹣200=10.
因为(a+b)2=a2+2ab+b2,所以a2+b2=(a+b)2﹣2ab=102﹣2×(﹣204)=508,
即(210﹣x)2+(x﹣200)2的值为508.
同学们,根据材料,请你完成下面这一题的解答过程:
“若x满足(2019﹣x)2+(2017﹣x)2=4044,试求(2019﹣x)(2017﹣x)的值”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线![]() 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为_______。
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为_______。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:
![]()
(1)将点B向右移动三个单位长度后到达点D,点D表示的数是 ;
(2)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请你直接写出所有点A移动的距离和方向;
(3)若A、B、C三个点移动后得到三个互不相等的有理数,它们既可以表示为1,![]() ,
,![]() 的形式,又可以表示为0,
的形式,又可以表示为0,![]() ,
,![]() 的形式,试求
的形式,试求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com