
【题目】某商场销售一种商品的进价为每件30元,销售过程中发现月销售量y(件)与销售单价x(元)之间的关系如图所示.
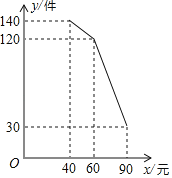
(1)根据图象直接写出y与x之间的函数关系式.
(2)设这种商品月利润为W(元),求W与x之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
【答案】(1)y=![]() ;(2)W=
;(2)W=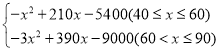 ;(3)这种商品的销售单价定为65元时,月利润最大,最大月利润是3675.
;(3)这种商品的销售单价定为65元时,月利润最大,最大月利润是3675.
【解析】
(1)当40≤x≤60时,设y与x之间的函数关系式为y=kx+b,当60<x≤90时,设y与x之间的函数关系式为y=mx+n,解方程组即可得到结论;
(2)当40≤x≤60时,当60<x≤90时,根据题意即可得到函数解析式;
(3)当40≤x≤60时,W=-x2+210x-5400,得到当x=60时,W最大=-602+210×60-5400=3600,当60<x≤90时,W=-3x2+390x-9000,得到当x=65时,W最大=-3×652+390×65-9000=3675,于是得到结论.
解:(1)当40≤x≤60时,设y与x之间的函数关系式为y=kx+b,
将(40,140),(60,120)代入得![]() ,
,
解得:![]() ,
,
∴y与x之间的函数关系式为y=﹣x+180;
当60<x≤90时,设y与x之间的函数关系式为y=mx+n,
将(90,30),(60,120)代入得![]() ,
,
解得:![]() ,
,
∴y=﹣3x+300;
综上所述,y=![]() ;
;
(2)当40≤x≤60时,W=(x﹣30)y=(x﹣30)(﹣x+180)=﹣x2+210x﹣5400,
当60<x≤90时,W=(x﹣30)(﹣3x+300)=﹣3x2+390x﹣9000,
综上所述,W=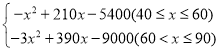 ;
;
(3)当40≤x≤60时,W=﹣x2+210x﹣5400,
∵﹣1<0,对称轴x=![]() =105,
=105,
∴当40≤x≤60时,W随x的增大而增大,
∴当x=60时,W最大=﹣602+210×60﹣5400=3600,
当60<x≤90时,W=﹣3x2+390x﹣9000,
∵﹣3<0,对称轴x=![]() =65,
=65,
∵60<x≤90,
∴当x=65时,W最大=﹣3×652+390×65﹣9000=3675,
∵3675>3600,
∴当x=65时,W最大=3675,
答:这种商品的销售单价定为65元时,月利润最大,最大月利润是3675.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:

时间t/h | 0 | 0.2 | 0.3 | 0.4 |
路程s/km |
(3)路程s可以看成时间t的函数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
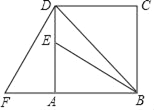
【题目】如图,在等边△BCD中,DF⊥BC于点F,点A为直线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.
(1)当点A在线段DF的延长线上时,
①求证:DA=CE;
②判断∠DEC和∠EDC的数量关系,并说明理由;
(2)当∠DEC=45°时,连接AC,求∠BAC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com