
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
【答案】(1)△ADO是直角三角形;(2)当α为110°、125°、140°时,三角形AOD是等腰三角形.
【解析】
试题分析:(1)首先根据已知条件可以证明△BOC≌△ADC,然后利用全等三角形的性质可以求出∠ADO的度数,由此即可判定△AOD的形状;
(2)利用(1)和已知条件及等腰三角形的性质即可求解.
试题解析:(1)∵△OCD是等边三角形,
∴OC=CD,
而△ABC是等边三角形,
∴BC=AC,
∵∠ACB=∠OCD=60°,
∴∠BCO=∠ACD,
在△BOC与△ADC中,
∵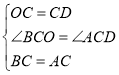 ,
,
∴△BOC≌△ADC,
∴∠BOC=∠ADC,
而∠BOC=α=150°,∠ODC=60°,
∴∠ADO=150°-60°=90°,
∴△ADO是直角三角形;
(2)∵设∠CBO=∠CAD=a,∠ABO=b,∠BAO=c,∠CAO=d,
则a+b=60°,b+c=180°-110°=70°,c+d=60°,a+d=50°∠DAO=50°,
∴b-d=10°,
∴(60°-a)-d=10°,
∴a+d=50°,
即∠CAO=50°,
①要使AO=AD,需∠AOD=∠ADO,
∴190°-α=α-60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO,
∴α-60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD,
∴190°-α=50°,
∴α=140°.
所以当α为110°、125°、140°时,三角形AOD是等腰三角形.


科目:初中数学 来源: 题型:
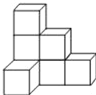
【题目】在桌面上,有7个完全相同的小正方体堆成的一个几何体A,如图所示.
(1) 请画出这个几何体A的三视图.
(2) 若将此几何体的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有______个.
(3) 若现在你的手头还有一些相同的小正方体可添放在该几何体上,要保持俯视图和左视图不变,则最多可以添加_______个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
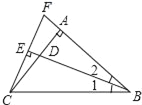
【题目】如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.CE=2,延长CE,BA交于点F.
(1)求证:△ADB≌△AFC;
(2)求BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC,
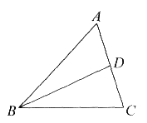
(1)作图:作BC边的垂直平分线分别交BC,BD于点E,F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接CF,若∠A=60°,∠ABD=24°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)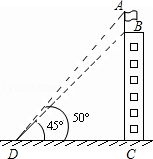
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;
x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;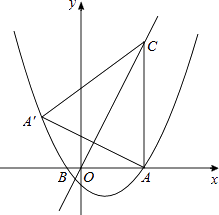
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图甲是任意一个直角三角形ABC,它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
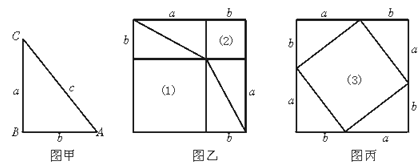
①图乙和图丙中(1)(2)(3)是否为正方形?为什么?
②图中(1)(2)(3)的面积分别是多少?
③图中(1)(2)的面积之和是多少?
④图中(1)(2)的面积之和与正方形(3)的面积有什么关系?为什么?
由此你能得到关于直角三角形三边长的关系吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=mx+10m与x轴负半轴、y轴正半轴分别交于A、B两点.
(1)当OA=OB时,试确定直线l的函数表达式;
(2)在(1)的条件下,如图2,设Q为直线AB上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=8,BN=6,求MN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图3.问:当点B在 y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
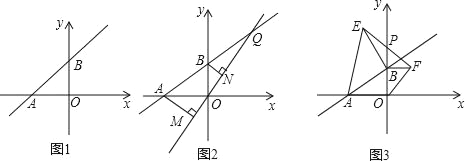
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.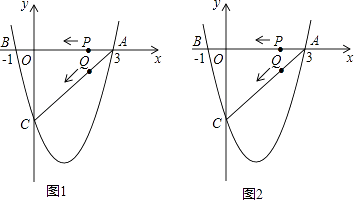
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com