
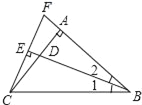
【题目】如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.CE=2,延长CE,BA交于点F.
(1)求证:△ADB≌△AFC;
(2)求BD的长度.
【答案】(1)证明见解析(2)4
【解析】
(1)先根据∠BAC=90°,可得:∠2+∠F=90°,∠ACF+∠F=90°,根据等角的余角相等可得:∠ACF=∠2,在△ABF和△ACD中,由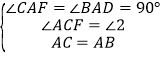 ,可判定△ACF≌△ABD.
,可判定△ACF≌△ABD.
(2)根据△ACF≌△ABD,可得BD=CF,再根据BE⊥CF,可得∠BEC=∠BEF=90°,
根据∠1+∠BCE=90°,∠2+∠F=90°,可得∠BCF=∠F,根据等角对等边可得:BC=BF,CE=EF=2,继而可得BD=CF=4.
(1)如图,
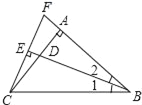
∵∠BAC=90°,
∴∠2+∠F=90°,∠ACF+∠F=90°,
∴∠ACF=∠2,
在△ABF和△ACD中,
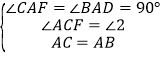 ,
,
∴△ACF≌△ABD.
(2)∵△ACF≌△ABD,
∴BD=CF,
∵BE⊥CF,
∴∠BEC=∠BEF=90°,
∵∠1+∠BCE=90°,∠2+∠F=90°,
∴∠BCF=∠F,
∴BC=BF,CE=EF=2,
∴BD=CF=4.


科目:初中数学 来源: 题型:
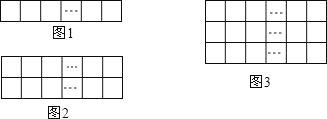
【题目】.现有 a 根长度相同的火柴棒,按如图 1 摆放时可摆成 m 个正方形,按如图 2摆放时可摆成 2n 个正方形.
(1)试分别用含 m,n 的代数式表示 a;
(2)若这 a 根火柴棒按如图 3 摆放时还可摆成 3p 个正方形.
①试问 p 的值能取 8 吗?请说明理由.
②试求 a 的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
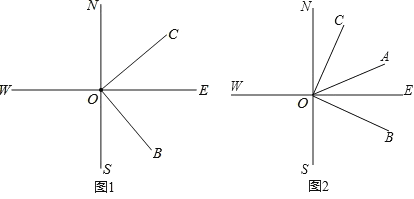
【题目】如图1,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向,已知射线OB的方向是南偏东m°,射线OC的方向为北偏东n°,且m°的角与n°的角互余.
(1)①若m=60,写出射线OC的方向.(直接回答)
②请直接写出图中所有与∠BOE互余的角及与∠BOE互补的角.
(2)如图2,若射线OA是∠BON的平分线,
①若m=70,求∠AOC的度数.
②若m为任意角度,求∠AOC的度数.(结果用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按下列方式搭建三角形:
![]() …
…
(1)填表:
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
(2)当三角形的个数为n时,火柴棒的根数是多少?
(3)求当n=1 000时,火柴棒的根数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为3.
时,该代数式的值为3.
(1)求c的值;
(2)已知:当![]() 时,该代数式的值为0.
时,该代数式的值为0.
①求:当![]() 时,该代数式的值;
时,该代数式的值;
②若![]() ,
,![]() ,
,![]() ,试比较a与d的大小,并说明理由.
,试比较a与d的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4…,若∠A=70°,则∠An﹣1AnBn﹣1(n>2)的度数为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com