练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠BAC=135°，AD⊥BC于D，且AB+BD=DC，那么∠C= °．

    【答案】15

    【解析】

    试题由AB+BD=DC，可以得到辅助线：在DC上截取DE=BD，连接AE；根据SAS证得△ADB≌△ADE，再利用全等三角形的对应边，对应角相等，可得到∠B=∠AED，AE=AB；又由等量代换，证得△AEC是等腰三角形，利用等边对等角，即可求得∠B与∠C的关系，由三角形的内角和是180°，即可求得结果．

    解：在DC上截取DE=BD，连接AE，

    ∵AD⊥BC，

    ∴∠ADB=∠ADE=90°，

    ∵AD=AD，

    ∴△ADB≌△ADE，

    ∴∠B=∠AED，AE=AB，

    ∵AB+BD=DC，DE+EC=DC，

    ∴AE=AB=EC，

    ∴∠AEB=2∠EAC=2∠C，

    ∴∠B=2∠C，

    ∵∠BAC=135°，∠B+∠C+∠BAC=180°，

    ∴3∠C=45°，

    ∴∠C=15°．

    故答案为：15．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小琳、晓明两人在100m的跑道上匀速跑步训练，他们同时从起点出发，跑向终点．

    （1）设小琳速度为v（m/s），写出小琳跑完全程所用的时间t（s）与速度v（m/s）之间的函数关系式；

    （2）已知晓明的速度是小琳速度的1.25倍，两人跑完全程，小琳要比晓明多用4s，用分式方程求小琳、晓明两人匀速跑步的速度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，OE平分∠AOC，OF平分∠BOC，且∠BOC=60°，若∠AOC+∠EOF=156°，则∠EOF的度数是（　　）

    A. 88° B. 30° C. 32° D. 48°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】盛盛同学到某高校游玩时，看到运动场的宣传栏中的部分信息（如下表）：

    院系篮球赛成绩公告

    比赛场次

    胜场

    负场

    积分

    22

    12

    10

    34

    22

    14

    8

    36

    22

    0

    22

    22

    盛盛同学结合学习的知识设计了如下问题，请你帮忙完成下列问题：

    （1）从表中可以看出，负一场积______分,胜一场积_______分；

    （2）某队在比完22场的前提下，胜场总积分能等于其负场总积分的2倍吗？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′的顶点都在格点上．

    （1）求证：△ABC∽A′B′C′；
    （2）A′B′C′与△ABC是位似图形吗？如果是，在图形上画出位似中心并求出位似比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

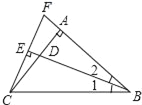
    【题目】如图所示，在△ABC中，AB=AC，∠BAC=90°，∠1=∠2，CE⊥BD交BD的延长线于点E．CE=2，延长CE，BA交于点F．

    （1）求证：△ADB≌△AFC；

    （2）求BD的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：点 A、B 在数轴上分别表示两个数 a、b，A、B 两点间的距离记为|AB|，O 表示原点当 A、B 两点中有一点在原点时，不妨设点 A 为原点， 如图 1，则|AB|=|OB|=|b|=|a﹣b|；当 A、B 两点都不在原点时，

    ①如图 2，若点 A、B 都在原点的右边时，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|

    ②如图 3，若点 A、B 都在原点的左边时，|AB|=|OB|﹣|OA|=|b|﹣|a|=|﹣b﹣（﹣a）=|a﹣b|；

    ③如图 4，若点 A、B 在原点的两边时，|AB|=|OB|+|OA|=|b|+|a|=﹣b+a=|a﹣b|． 回答下列问题：综上所述，数轴上 A、B 两点间的距离为|AB|=|a﹣b|

    (1)若数轴上的点 A 表示的数为﹣1，点 B 表示的数为 9，则 A、B 两点间的距离为

    (2)若数轴上的点 A 表示的数为﹣1，动点 P 从点 A 出发沿数轴正方向运动， 点 P 的速度是每秒 4 个单位长度，t 秒后点 P 表示的数可表示为

    (3)若点 A 表示的数﹣1，点 B 表示的数 9，动点 P、Q 分别同时从 A、B 出发沿数轴正方向运动，点 P 的速度是每秒 4 个单位长度，点 Q 的速度是每秒 2 个单位长度，求：运动几秒时，点 P 可以追上点 Q？（请写出必要的求解过程）

    (4)若点 A 表示的数﹣1，点 B 表示的数 9，动点 P、Q 分别同时从 A、B 出发沿数轴正方向运动，点 P 的速度是每秒 4 个单位长度，点 Q 的速度是每秒 2 个单位长度，求运动几秒时，P、Q 两点相距 5 个单位长度？（请写出必要的求解过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】测量计算是日常生活中常见的问题，如图，建筑物BC的屋顶有一根旗杆AB，从地面上D点处观测旗杆顶点A的仰角为50°，观测旗杆底部B点的仰角为45°，（可用的参考数据：sin50°≈0.8，tan50°≈1.2）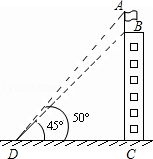

    （1）若已知CD=20米，求建筑物BC的高度；
    （2）若已知旗杆的高度AB=5米，求建筑物BC的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列函数中，当x＞0时，y的值随x的值增大而减小的函数是（ ）
    A.y=3x
    B.y=x﹣1
    C.y=
    D.y=2x2

    查看答案和解析>>

    同步练习册答案