
【题目】阅读下面材料:点 A、B 在数轴上分别表示两个数 a、b,A、B 两点间的距离记为|AB|,O 表示原点当 A、B 两点中有一点在原点时,不妨设点 A 为原点, 如图 1,则|AB|=|OB|=|b|=|a﹣b|;当 A、B 两点都不在原点时,
①如图 2,若点 A、B 都在原点的右边时,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
②如图 3,若点 A、B 都在原点的左边时,|AB|=|OB|﹣|OA|=|b|﹣|a|=|﹣b﹣(﹣a)=|a﹣b|;
③如图 4,若点 A、B 在原点的两边时,|AB|=|OB|+|OA|=|b|+|a|=﹣b+a=|a﹣b|. 回答下列问题:综上所述,数轴上 A、B 两点间的距离为|AB|=|a﹣b|
(1)若数轴上的点 A 表示的数为﹣1,点 B 表示的数为 9,则 A、B 两点间的距离为
(2)若数轴上的点 A 表示的数为﹣1,动点 P 从点 A 出发沿数轴正方向运动, 点 P 的速度是每秒 4 个单位长度,t 秒后点 P 表示的数可表示为
(3)若点 A 表示的数﹣1,点 B 表示的数 9,动点 P、Q 分别同时从 A、B 出发沿数轴正方向运动,点 P 的速度是每秒 4 个单位长度,点 Q 的速度是每秒 2 个单位长度,求:运动几秒时,点 P 可以追上点 Q?(请写出必要的求解过程)

(4)若点 A 表示的数﹣1,点 B 表示的数 9,动点 P、Q 分别同时从 A、B 出发沿数轴正方向运动,点 P 的速度是每秒 4 个单位长度,点 Q 的速度是每秒 2 个单位长度,求运动几秒时,P、Q 两点相距 5 个单位长度?(请写出必要的求解过程)
【答案】(1)10;(2) 4t﹣1;(3) 运动 5 秒时,点 P 可以追上点 Q;(4) 运动![]() 秒或者
秒或者![]() 秒时,P,Q 两点相距 5 个单位长度
秒时,P,Q 两点相距 5 个单位长度
【解析】
(1)由|AB|=|a﹣b|即可计算;
(2)t 秒后点 P运动的距离为4t,由于P是正方向运动且起点为-1,则P点可表示为4t﹣1;
(3)设运动 x 秒时,点 P 可以追上点 Q,则P的速度为4x,Q的速度为2x,根据题意可知,相遇时P所在的位置为4x﹣1,Q所在的位置为2x+9,据此列方程解答即可;
(4)分点P在点Q左侧和右侧两种情况分别讨论即可.
(1)∵点 A 表示的数为﹣1,点 B 表示的数为 9,
∴|AB|=|﹣1﹣9|=10.
故答案为:10.
(2)∵点 P 运动的速度为每秒4个单位长度,出发点为﹣1,
∴t 秒后点 P 表示的数为 4t﹣1.
故答案为:4t﹣1.
(3)设运动x秒时,点P可以追上点Q,根据题意得:4x﹣1=2x+9,
解得:x=5,
答:运动 5 秒时,点 P 可以追上点 Q.
(4)设运动 y 秒时,P,Q 两点相距 5 个单位长度.
当点 P 在点 Q 左侧时,(2y+9)﹣(4y﹣1)=5,
解得:y=![]() ;
;
当点 P 在点 Q 右侧时,(4y﹣1)﹣(2y+9)=5,解得:y=![]() .
.
答:运动![]() 秒或者
秒或者![]() 秒时,P,Q 两点相距 5 个单位长度.
秒时,P,Q 两点相距 5 个单位长度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为﹣10和6,动点P从点A出发,以每秒6个单位长度的速度沿数轴正方向匀速运动,同时动点Q从点B出发,以每秒3个单位的速度沿数轴负方向匀速运动,设运动时间为t(t>0)秒
(1)当t=2时,求AP的中点C所对应的数;
(2)当PQ=OA时,求点Q所对应的数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是 , △ABC的面积为 . 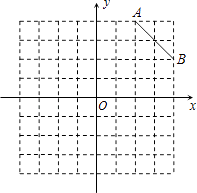
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4…,若∠A=70°,则∠An﹣1AnBn﹣1(n>2)的度数为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.

(1)求证:AD=DC;
(2)如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC中,∠C=90°.
(1)若a=5,b=12,则c=________;
(2)若a=6,c=10,则b=_______;
(3)若a∶b=3∶4,c=10,则a=_______,b=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形OABC的边OC=2,将过点B的直线y=x﹣3与x轴交于点E.
(1)求点B的坐标;
(2)连结CE,求线段CE的长;
(3)若点P在线段CB上且OP=![]() ,求P点坐标.
,求P点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com