Question

【题目】在等边△ABC中，点D在BC边上（不与点B、点C重合），点E在AC的延长线上，DE=DA（如图1）．

（1）求证：∠BAD=∠EDC；

（2）点E关于直线BC的对称点为M，连接DM，AM．

①依题意将图2补全；

②若点D在BC边上运动，DA与AM始终相等吗？请说明理由．

Answer 1

【答案】证明见解析

【解析】

（1）因为DE=DA,,根据等边对等角可得:∠E=∠DAC,由△ABC是等边三角形,可得∠BAC=∠ACD=60°,即∠BAD+∠DAC=∠E+∠EDC=60°,进而可得:∠BAD=∠EDC,

（2）②证法1:由轴对称可得,DM=DE,∠EDC=∠MDC,

由DE=DA,可得:DM=DA,由（1）可得,∠BAD=∠EDC,等量代换可得:∠MDC=∠BAD,

因为在△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,可证得:∠MDC+∠ADB=120°,继而可得:

∠ADM=180°﹣120°=60°,可得:△ADN是等边三角形,所以AD=AM,

证法2:连接CM,由轴对称可得,DM=DE,∠EDC=∠MDC,

由DE=DA,等量代换可得:DM=DA,由（1）可得,∠BAD=∠EDC,等量代换可得:

∠MDC=∠BAD,因为在△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,

可得:∠MDC+∠ADB=120°,进而可得:∠ADM=180°﹣120°=60°,故△ADM中,∠DAM=（180°﹣60°）÷2=60°,根据∠BAC=60°,可得∠BAD=∠CAM,由轴对称可得,∠DCE=∠DCM=120°,

又因为∠ACB=60°,所以∠ACM=120°﹣60°=60°,即∠B=∠ACM,

在△ABD和△ACM中,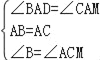,可判定△ABD≌△ACM（ASA）,所以AD=AM．

（1）如图1,

∵DE=DA,

∴∠E=∠DAC,

∵△ABC是等边三角形,

∴∠BAC=∠ACD=60°,

即∠BAD+∠DAC=∠E+∠EDC=60°,

∴∠BAD=∠EDC,

（2）①补全图形如图2,

②证法1:由轴对称可得,DM=DE,∠EDC=∠MDC,

∵DE=DA,

∴DM=DA,

由（1）可得,∠BAD=∠EDC,

∴∠MDC=∠BAD,

∵△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,

∴∠MDC+∠ADB=120°,

∴∠ADM=180°﹣120°=60°,

∴△ADN是等边三角形,

∴AD=AM,

证法2:连接CM,

由轴对称可得,DM=DE,∠EDC=∠MDC,

∵DE=DA,

∴DM=DA,

由（1）可得,∠BAD=∠EDC,

∴∠MDC=∠BAD,

∵△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,

∴∠MDC+∠ADB=120°,

∴∠ADM=180°﹣120°=60°,

∴△ADM中,∠DAM=（180°﹣60°）÷2=60°,

又∵∠BAC=60°,

∴∠BAD=∠CAM,

由轴对称可得,∠DCE=∠DCM=120°,

又∵∠ACB=60°,

∴∠ACM=120°﹣60°=60°,

∴∠B=∠ACM,

在△ABD和△ACM中,

,

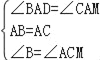∴△ABD≌△ACM（ASA）,

∴AD=AM．