
【题目】如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.
(1)求证:△ABC∽A′B′C′;
(2)A′B′C′与△ABC是位似图形吗?如果是,在图形上画出位似中心并求出位似比.
【答案】
(1)
证明:∵AB= ![]() ,BC=
,BC= ![]() ,AC=2
,AC=2 ![]() ,A′B′=2
,A′B′=2 ![]() ,B′C′=2
,B′C′=2 ![]() ,A′C′=4
,A′C′=4 ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴△ABC∽A′B′C′
(2)
解:如图所示:两三角形对应点的连线相交于一点,故A′B′C′与△ABC是位似图形,O即为位似中心,
位似比为:2.

【解析】(1)分别求出三角形各边长,进而得出答案;(2)利用位似图形的性质得出答案.
【考点精析】根据题目的已知条件,利用作图-位似变换的相关知识可以得到问题的答案,需要掌握对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.


科目:初中数学 来源: 题型:
【题目】列方程解应用题:
(1)一个箱子,如果装橙子可以装18个,如果装梨可以装16个,现共有橙子、梨400个,而且装梨的箱子是装橙子箱子的2倍.请算一下,装橙子和装梨的箱子各多少个?
(2)一群小孩分一堆苹果,每人3个多7个,每人4个少3个,求有几个小孩?几个苹果?
(3)一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的速度和两城之间的航程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是 , △ABC的面积为 . 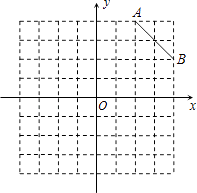
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() 和一次函数y=﹣x+a﹣2(a为常数)
和一次函数y=﹣x+a﹣2(a为常数)
(1)当a=0时,求反比例函数与一次函数的交点坐标.
(2)当反比例函数与一次函数有两个交点时,请确定a的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.

(1)求证:AD=DC;
(2)如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
高斯是德国著名的大科学家,他最出名的故事就是在他10岁时,小学老师出了一道算术难题:计算1+2+3+……+100=?
在其他同学还在犯难时,却很快传来了高斯的声音:“老师,我已经算好了!”
老师很吃惊,高斯解释道:因为1+100=101,2+99=101,3+98=101,……,49+52=101,50+51=101,而像这样的等于101的组合一共有50组,所以答案很快就可以求出:101×50=5050。
根据以上的信息,请同学们:
(1)计算1+3+5+7+…+99的值.
(2)计算2+4+6+8+…+200的值.
(3)用含a和n的式子表示运算结果:求a+2a+3a+…+na的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com