
【题目】已知反比例函数y= ![]() 和一次函数y=﹣x+a﹣2(a为常数)
和一次函数y=﹣x+a﹣2(a为常数)
(1)当a=0时,求反比例函数与一次函数的交点坐标.
(2)当反比例函数与一次函数有两个交点时,请确定a的范围.
【答案】
(1)解:当a=0时,一次函数y=﹣x+a﹣2的解析式是y=﹣x﹣2,
联立反比例函数解析式、一次函数解析式,得  ,
,
解得 ![]() .
.
故当a=0时,反比例函数与一次函数的交点坐标是(﹣1,﹣1)
(2)解:存在实数a,使反比例函数与一次函数有两个交点,
联立反比例函数解析式、一次函数解析式,得  .
.
由方程组有2组解,得
x2﹣(a﹣2)x+1=0有两个不相等的实数根.
△=[﹣(a﹣2)]2﹣4>0,
解得a<0或a>4.
故a的范围是a<0或a>4
【解析】(1)根据a的值,可得一次函数的解析式,联立反比例函数与一次函数的解析式,可得方程组,解方程组,可得交点坐标;(2)联立反比例函数与一次函数的解析式,可得方程组,根据反比例函数与一次函数有两个交点,可得方程组有2组解,根据一元二次方程的判别式,可得答案.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=2![]() ,AC=2,求四边形AODE的周长.
,AC=2,求四边形AODE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线MN是等边△ABC底边BC的中垂线,点P在直线MN上,且使△PAB、△PAC、△PBC都是等腰三角形,满足上述条件的点P的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 . 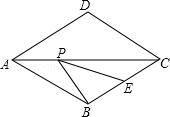
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.
(1)求证:△ABC∽A′B′C′;
(2)A′B′C′与△ABC是位似图形吗?如果是,在图形上画出位似中心并求出位似比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中考体育测试有“跳绳”项目,为加强训练,某班女生分成甲、乙两组参加班级跳绳对抗赛,两组参赛人数相等,比赛结束后,依据两组学生的成绩(满分为10分)绘制了如下统计图表:
甲组学生成绩统计表
分 数 | 人 数 |
5分 | 5人 |
6分 | 2人 |
7分 | 3人 |
8分 | 1人 |
9分 | 4人 |

(1)经计算,乙组的平均成绩为7分,中位数是6分,请求出甲组学生的平均成绩、中位数,并从平均数的角度分析哪个组的成绩较好?
(2)经计算,甲组的成绩的方差是2.56,乙组的方差是多少?比较可得哪个组的成绩较为整齐?
(3)学校组织跳绳比赛,班主任决定从这次对抗赛中得分为9分的学生中抽签选取5个人组成代表队参赛,则在对抗赛中得分为9分的学生参加比赛的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.

(1)求证:BE=BF;
(2)若△ABC的面积为70,AB=16,DE=5,则BC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=﹣x+b与直线l2:y=kx+1相交于点A(1,3).
(1)求直线l1、l2的函数表达式;
(2)求直线l1、l2和x轴围成的三角形ABC的面积;
(3)求直线l1、l2与坐标轴围成的四边形ABOD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com