【题目】已知，直线MN是等边△ABC底边BC的中垂线，点P在直线MN上，且使△PAB、△PAC、△PBC都是等腰三角形，满足上述条件的点P的个数有（ ）
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解：如图所示，作BC的垂直平分线，①△ABC的外心P1为满足条件的一个点， ②以点A为圆心，以AB长为半径画圆，P2、P3为满足条件的点，
③分别以点C、B为圆心，以AB长为半径画圆，P4为满足条件的点，
综上所述，满足条件的所有点P的个数为4．
故选D．
【考点精析】通过灵活运用线段垂直平分线的性质和等腰三角形的判定，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等即可以解答此题．
科目：初中数学 来源： 题型：
【题目】列方程解应用题：五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
倍多15件，甲、乙两种商品的进价和售价如下表（注：获利=售价﹣进价）
甲 | 乙 | |
进价（元/件） | 20 | 30 |
售价（元/件） | 29 | 40 |
（1）新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（2）该购物中心第二次以第一次的进价又购进甲、乙两种商品，其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元，求第二次乙种商品是按原价打几折销售？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（10分）如图，△ABC中，边AB、AC的垂直平分线分别交BC于D、E．
（1）若BC=10，则△ADE周长是多少？为什么？
（2）若∠BAC=128°，则∠DAE的度数是多少？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某人到岛上去探宝，从A处登陆后先往东走4 km，又往北走1.5 km，遇到障碍后又往西走2 km，再折回向北走到4.5 km处往东一拐，仅走0.5 km就找到宝藏．问登陆点A与宝藏埋藏点B之间的距离是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．C点的坐标是 ， △ABC的面积为 ．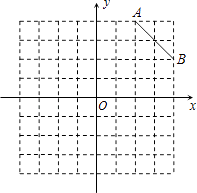 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知反比例函数y= 
和一次函数y=﹣x+a﹣2（a为常数）
（1）当a=0时，求反比例函数与一次函数的交点坐标．
（2）当反比例函数与一次函数有两个交点时，请确定a的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在等边△ABC中，点D在BC边上（不与点B、点C重合），点E在AC的延长线上，DE=DA（如图1）．
（1）求证：∠BAD=∠EDC；
（2）点E关于直线BC的对称点为M，连接DM，AM．
①依题意将图2补全；
②若点D在BC边上运动，DA与AM始终相等吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的倍多15件，甲、乙两种商品的进价和售价如下表（注：获利=售价﹣进价）
甲 | 乙 | |
进价（元/件） | 20 | 30 |
售价（元/件） | 29 | 40 |
（1）新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（2）该购物中心第二次以第一次的进价又购进甲、乙两种商品，其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元，求第二次乙种商品是按原价打几折销售？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
