
����Ŀ����ͼ1��ֱ��SN��ֱ��WE�ཻ�ڵ�O������ON��ʾ������������OE��ʾ����������֪����OB�ķ�������ƫ��m��������OC�ķ���Ϊ��ƫ��n������m���Ľ���n���Ľǻ�����
��1������m=60��д������OC�ķ���ֱ�ӻش���
����ֱ��д��ͼ���������BOE����ĽǼ����BOE�����Ľǣ�
��2����ͼ2��������OA�ǡ�BON��ƽ���ߣ�
����m=70�����AOC�Ķ�����
����mΪ����Ƕȣ����AOC�Ķ�����������ú�m��ʽ�ӱ�ʾ��
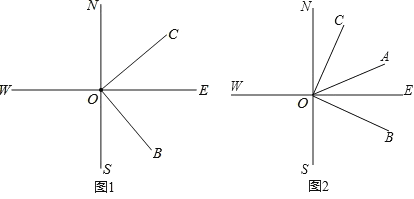
���𰸡���1���ٱ�ƫ��30�㣻�����BOE����Ľ��С�BOS����COE�����BOE�����Ľ��С�BOW����COS����2����35�㣻�ڡ�AOC=![]() m�㣮
m�㣮
��������
��1����������ǵĶ������n��ֵ��Ȼ����ݷ���ǵĶ��弴�ɽ��
��������ǺͲ��ǵĶ��弴�ɽ��
��2�������������BON�Ķ�����Ȼ����ݽ�ƽ���ߵĶ��������AON��Ȼ�������AOC=��AON-��CON������⣻
���ⷨ������ͬ����70���ij�m����������⣮
��1���ٱ�ƫ��30�㣬
�⣺n=90�㩁60��=30����������OC�ķ����ǣ���ƫ��30��
�����BOE����Ľ��С�BOS����COE��
���BOE�����Ľ��С�BOW����COS��
��2����35�㣻
�⣺��BON=180�㩁70��=110�㣬
��OA�ǡ�BON��ƽ���ߣ�
���AON=![]() ��BON=55�㣬
��BON=55�㣬
�֡ߡ�CON=90�㩁70��=20�㣬
���AOC=��AON����CON=55�㩁20��=35�㣮
�ڡߡ�BOS+��BON=180�㣬
���BOS=180�㩁��BON=180�㩁m�㣮
��OA�ǡ�BON��ƽ���ߣ�
���AON=![]() ��BON=
��BON=![]() ��180�㩁m�㣩=90�㩁
��180�㩁m�㣩=90�㩁![]() m�㣮
m�㣮
�ߡ�BOS+��CON=m��+n��=90�㣬
���CON=90�㩁m�㣬
���AOC=��AON����CON=90�㩁![]() m�㩁��90�㩁m�㣩=90�㩁
m�㩁��90�㩁m�㣩=90�㩁![]() m�㩁90��+m��=
m�㩁90��+m��=![]() m�㣮
m�㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1�����ڡ�ABC�У�AD��BC�ߵ����ߣ���A����AE��BC���D����DE��AB���ڵ�E������CE�� 
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2������BE��AC�ֱ���BE��DE���ڵ�F��G����ͼ��2������AC=6����FG�ij��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AB=4cm������P��1cm/s���ٶȷֱ�ӵ�A��Bͬʱ��������P��A��B���յ�B�˶�����Q��B��A���յ�A�˶�������P��PD��AC�ڵ�D����PDΪ�����Ҳ���������PDEF������Q��QG��AB��������BC��CA�ڵ�G���C���غϣ���QGΪ��������ֱ�ǡ�QGH���ҵ�GΪֱ�Ƕ��㣬��C��Hʼ����QG��ͬ�࣬��������PDEF���QGH�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����0��t��4����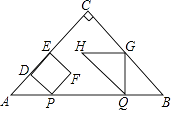
��1������F�ڱ�QH��ʱ����t��ֵ��
��2����������PDEF���QGH�ص�����ͼ�����ı���ʱ����S��t֮��ĺ�����ϵʽ��
��3����FH���ڵ�ֱ��ƽ�л�ֱ��ABʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
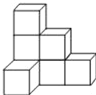
����Ŀ���������ϣ���7����ȫ��ͬ��С������ѳɵ�һ��������A����ͼ��ʾ.
(1) �뻭�����������A������ͼ.
(2) �����˼�����ı������Ϻ���(���������ϵ�һ�治��)�������������Ǻ�ɫ��С��������______��.
(3) �����������ͷ����һЩ��ͬ��С������������ڸü������ϣ�Ҫ���ָ���ͼ������ͼ���䣬������������_______��С������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OEƽ�֡�AOC��OFƽ�֡�BOC���ҡ�BOC=60��������AOC+��EOF=156�������EOF�Ķ����ǣ�������

A. 88�� B. 30�� C. 32�� D. 48��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������û�е��ܱ�ʾ![]() +1�����������ǿ��������������۴�����С��ʵ������4��ƽ�����ǡ�2����ʽ�ӱ�ʾ��
+1�����������ǿ��������������۴�����С��ʵ������4��ƽ�����ǡ�2����ʽ�ӱ�ʾ��![]() =��2����ij���ľ���ֵ���෴��������ƽ�������������������������0��������ȷ����______��
=��2����ij���ľ���ֵ���෴��������ƽ�������������������������0��������ȷ����______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʢʢͬѧ��ij��У����ʱ�������˶������������еIJ�����Ϣ�����±�����
Ժϵ�������ɼ����� | |||
�������� | ʤ�� | ���� | ���� |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
ʢʢͬѧ���ѧϰ��֪ʶ������������⣬�����æ����������⣺
��1���ӱ��п��Կ�������һ����______��,ʤһ����_______����
��2��ij���ڱ���22����ǰ���£�ʤ���ܻ����ܵ����为���ܻ��ֵ�2������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
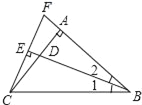
����Ŀ����ͼ��ʾ������ABC�У�AB=AC����BAC=90�㣬��1=��2��CE��BD��BD���ӳ����ڵ�E��CE=2���ӳ�CE��BA���ڵ�F��
��1����֤����ADB�ա�AFC��
��2����BD�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������һ��ֱ��������ABC����������ֱ�DZߵı߳��ֱ�Ϊa��b,б�߳�Ϊc.��ͼ�ҡ��������ֱ�ȡ�ĸ���ֱ��������ABCȫ�ȵ������Σ����ڱ߳�Ϊa+b����������.
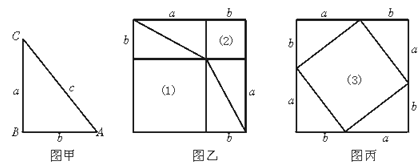
��ͼ�Һ�ͼ���У�1����2����3���Ƿ�Ϊ�����Σ�Ϊʲô��
��ͼ�У�1����2����3��������ֱ��Ƕ��٣�
��ͼ�У�1����2�������֮���Ƕ��٣�
��ͼ�У�1����2�������֮���������Σ�3���������ʲô��ϵ��Ϊʲô��
�ɴ����ܵõ�����ֱ�����������߳��Ĺ�ϵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com