
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AB=4cm,动点P以1cm/s的速度分别从点A、B同时出发,点P沿A→B向终点B运动,点Q沿B→A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC﹣CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4).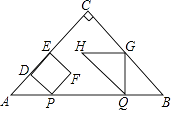
(1)当点F在边QH上时,求t的值;
(2)当正方形PDEF与△QGH重叠部分图形是四边形时,求S与t之间的函数关系式;
(3)当FH所在的直线平行或垂直于AB时,直接写出t的值.
【答案】
(1)
解:如图1中,当点F在边QH上时,易知AP=PQ=BQ,
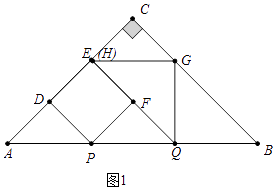
∵Rt△ABC中,AB=4,
∴t= ![]() 时,点F在边QH上
时,点F在边QH上
(2)
解:如图2中,当点F在GQ上时,易知AP=BQ=t,PD=PF= ![]() t.PQ=PF=
t.PQ=PF= ![]() t,
t,

∴t+ ![]() t+t=4,
t+t=4,
∴t= ![]() ,
,
由(1)可知,当 ![]() <t≤
<t≤ ![]() 时,正方形PDEF与△QGH重叠部分图形是四边形
时,正方形PDEF与△QGH重叠部分图形是四边形
此时s= ![]() t[
t[ ![]() t﹣
t﹣ ![]() (4﹣2t)]=
(4﹣2t)]= ![]() t2﹣2t.
t2﹣2t.
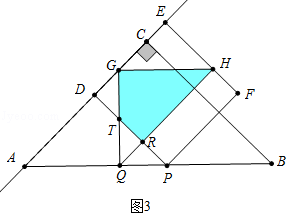
如图3中,当G在EF上时,则有 ![]() (4﹣t)=
(4﹣t)= ![]() t+
t+ ![]() (2t﹣4).解得t=
(2t﹣4).解得t= ![]() ,
,
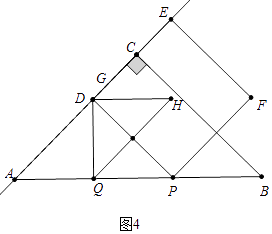
如图4中,当G与D重合时,易知2t﹣4= ![]() t,解得t=
t,解得t= ![]() .
.
当 ![]() ≤t<
≤t< ![]() 时,S=S△GHQ﹣S△TRQ=
时,S=S△GHQ﹣S△TRQ= ![]() (4﹣t)2﹣
(4﹣t)2﹣ ![]() [
[ ![]() (2t﹣4)]2=﹣
(2t﹣4)]2=﹣ ![]() t2﹣4
t2﹣4
(3)
解:①如图5中,当FH⊥AB时,延长HF交AB于T,易知AP=BQ=GQ=HG=TQ=t,PT= ![]() t,
t,
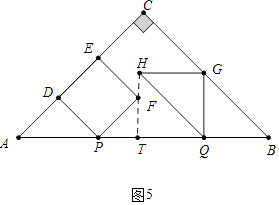
∴3t+ ![]() t=4,
t=4,
∴t= ![]() .
.
②如图7中,当HF⊥AB于T时,
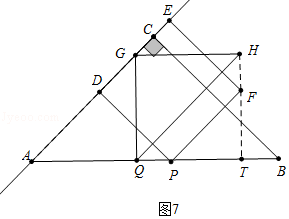
∵TB=4﹣2(4﹣t)=4﹣ ![]() t,解得t=
t,解得t= ![]() ,
,
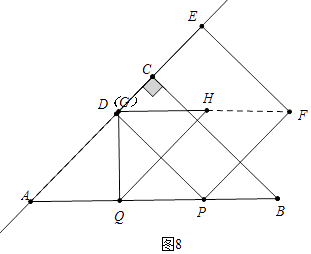
③如图8中,当HF∥AB时,∴ ![]() t+t=4,
t+t=4,
∴t= ![]() ,
,
综上所述,t= ![]() s或
s或 ![]() s或
s或 ![]() 时,FH所在的直线平行或垂直于AB
时,FH所在的直线平行或垂直于AB
【解析】(1)如图1中,当点F在边QH上时,易知AP=PQ=BQ,求出AB的长即可解决问题;(2)分两种情形①如图2中,当点F在GQ上时,易知AP=BQ=t,PD=PF= ![]() t.PQ=PF=
t.PQ=PF= ![]() t,列出方程即可解决问题;②如图3中,重叠部分是四边形GHRT时;(3)分三种种情形求解①如图5中,当FH⊥AB时,延长HF交AB于T,易知AP=BQ=GQ=HG=TQ=t,PT=
t,列出方程即可解决问题;②如图3中,重叠部分是四边形GHRT时;(3)分三种种情形求解①如图5中,当FH⊥AB时,延长HF交AB于T,易知AP=BQ=GQ=HG=TQ=t,PT= ![]() t;②如图7中,当FH∥AB时,易知AQ=PQ=
t;②如图7中,当FH∥AB时,易知AQ=PQ= ![]() t,BQ=t;分别列出方程即可解决问题.③如图8中,当HF∥AB时;
t,BQ=t;分别列出方程即可解决问题.③如图8中,当HF∥AB时;


科目:初中数学 来源: 题型:
【题目】骑自相车旅行越来越受到人们的喜爱,顺风车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%. A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
(1)求今年4月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+5与x轴交于A(1,0)、B(5,0)两点,点D是抛物线上横坐标为6的点.点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线AD交于点Q,过点Q作QF垂直于y轴,点F在点Q的右侧,且QF=2,以QF、QP为邻边作矩形QPEF.设矩形QPEF的周长为d,点P的横坐标为m.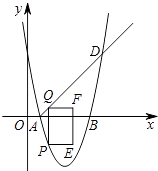
(1)求这条抛物线所对应的函数表达式.
(2)求这条抛物线的对称轴将矩形QPEF的面积分为1:2两部分时m的值.
(3)求d与m之间的函数关系式及d随m的增大而减小时d的取值范围.
(4)当矩形QPEF的对角线互相垂直时,直接写出其对称中心的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
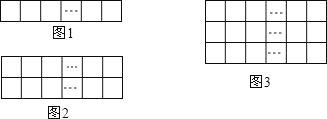
【题目】.现有 a 根长度相同的火柴棒,按如图 1 摆放时可摆成 m 个正方形,按如图 2摆放时可摆成 2n 个正方形.
(1)试分别用含 m,n 的代数式表示 a;
(2)若这 a 根火柴棒按如图 3 摆放时还可摆成 3p 个正方形.
①试问 p 的值能取 8 吗?请说明理由.
②试求 a 的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为﹣10和6,动点P从点A出发,以每秒6个单位长度的速度沿数轴正方向匀速运动,同时动点Q从点B出发,以每秒3个单位的速度沿数轴负方向匀速运动,设运动时间为t(t>0)秒
(1)当t=2时,求AP的中点C所对应的数;
(2)当PQ=OA时,求点Q所对应的数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车与B地的路程分别为 y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)a= ;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;
(3)若a≤x≤5,则当x为何值时,两车相距100km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,直线AB与x轴负半轴交于点A(a,0),与 y轴正半轴交于点B(0,b),且![]() +|b﹣4|=0.
+|b﹣4|=0.

(1)求△AOB的面积;
(2)如图2,若P为直线AB上一动点,连接OP,且2S△AOP≤S△BOP≤3S△AOP,求P点横坐标xP的取值范围;
(3)如图3,点C在第三象限的直线AB上,连接OC,OE⊥OC于O,连接CE交y 轴于点D,连接AD交OE的延长线于F,则∠OAD、∠ADC、∠CEF、∠AOC之间是否有某种确定的数量关系?试证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
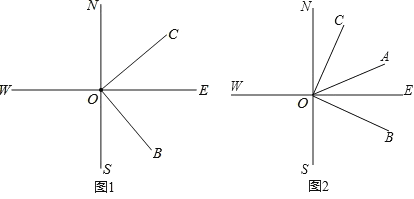
【题目】如图1,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向,已知射线OB的方向是南偏东m°,射线OC的方向为北偏东n°,且m°的角与n°的角互余.
(1)①若m=60,写出射线OC的方向.(直接回答)
②请直接写出图中所有与∠BOE互余的角及与∠BOE互补的角.
(2)如图2,若射线OA是∠BON的平分线,
①若m=70,求∠AOC的度数.
②若m为任意角度,求∠AOC的度数.(结果用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4…,若∠A=70°,则∠An﹣1AnBn﹣1(n>2)的度数为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com