
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�ֱ��AB��x�Ḻ���ύ�ڵ�A��a��0������ y�������ύ�ڵ�B��0��b������![]() +|b��4|=0��
+|b��4|=0��

��1�����AOB�������
��2����ͼ2����PΪֱ��AB��һ���㣬����OP����2S��AOP��S��BOP��3S��AOP����P�������xP��ȡֵ��Χ��
��3����ͼ3����C�ڵ�������ֱ��AB�ϣ�����OC��OE��OC��O������CE��y ���ڵ�D������AD��OE���ӳ�����F�����OAD����ADC����CEF����AOC֮���Ƿ���ij��ȷ����������ϵ����֤����Ľ��ۣ�
���𰸡���1��12����2����4.5��xP�ܩ�4��12��xP�ܩ�9����3����CEF+��ADC����OAD����AOC=90�㣮
��������
��1�����÷Ǹ��������ʼ��ɽ�����⣻
��2������P��PH��y����H����PH=|xP|���������������ۼ��ɢٵ�P�ڵ�һ����ʱ��S��BOP��S��AOP�����۲��������ڵ�P�ڵڶ�����ʱ��PH=|xP|=-xP��S��BOP=-2xP��S��AOP=12+2xP���г�����ʽ���ɽ�����⣮��P�ڵ�������ʱ���г�����ʽ���ɣ�
��3����ͼ����AM��OF��CD��M��DN��OF��OC��N������ƽ���ߵ����ʣ���ʽ�����ʼ��ɽ������.
��1����![]() +|b��4|=0��
+|b��4|=0��
�֡�![]() ��0��|b��4|��0��
��0��|b��4|��0��
��a=��6��b=4��
��A����6��0����B��0��4��
��S��AOB=![]() ��6��4=12��
��6��4=12��
��2����ͼ������P��PH��y����H����PH=|xP|����ͼ�ο�֪��
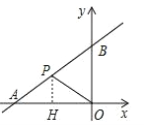
�ٵ�P�ڵ�һ����ʱ��S��BOP��S��AOP�����۲�������
�ڵ�P�ڵڶ�����ʱ��PH=|xP|=��xP��S��BOP=��2xP��S��AOP=12+2xP
��2��12+2xP���ܩ�2xP��3��12+2xP����
��é�4.5��xP�ܩ�4��
��P�ڵ�������ʱ��2����2xP��12���ܩ�2xP��3����2xP��12����
��é�12��xP�ܩ�9��
���ϣ�P�������xP��ȡֵ��Χ�ǩ�4.5��xP�ܩ�4��12��xP�ܩ�9��
��3����ͼ����AM��OF��CD��M��DN��OF��OC��N��
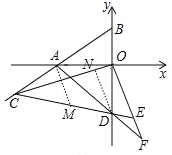
��AM��OF��DN��
���AMD=��CEF����ADN=��DAM����AMD+��ADC+��ADN=180������
��FOC+��AOC+��OAD+��DAM=180�㣬
�֡ߡ�FOC=90�㣬
���OAD+��AOC+��DAM=90������
�ɢٵá�ADN=180�㩁��AMD����ADC���ɢڵá�DAM=90�㩁��OAD����AOC��
�֡�ADN=��DAM��
��180�㩁��AMD����ADC=90�㩁��OAD����AOC��
�֡ߡ�AMD=��CEF��
���CEF+��ADC����OAD����AOC=90�㣮
�����CEF+��ADC=90��+��OAD+��AOC���ƽ��۾��ɣ�


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У�BC��AC����ACB��90�㣬DΪ����AB��һ�㣬����CD������C���߶�CD�Ĵ���l����ֱ��l�ϣ��ֱ��ڵ�C�������ȡ���߶�CD��ȵ��߶�CE��CF������AE��BF.
(1)����D���߶�AB��ʱ(��D�����A��B�غ�)����ͼ23(a)��
�����㽫ͼ�β���������
���߶�BF��AD����ֱ�ߵ�λ�ù�ϵΪ________���߶�BF��AD��������ϵΪ________��
(2)����D���߶�AB���ӳ�����ʱ����ͼ23(b)��
��(1)�Т��ʵĽ����Ƿ���Ȼ��������������������֤�����������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ա�����������100m���ܵ��������ܲ�ѵ��������ͬʱ���������������յ㣮
��1����С���ٶ�Ϊv��m/s����д��С������ȫ�����õ�ʱ��t��s�����ٶ�v��m/s��֮��ĺ�����ϵʽ��
��2����֪�������ٶ���С���ٶȵ�1.25������������ȫ�̣�С��Ҫ����������4s���÷�ʽ������С�ա��������������ܲ����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AB=4cm������P��1cm/s���ٶȷֱ�ӵ�A��Bͬʱ��������P��A��B���յ�B�˶�����Q��B��A���յ�A�˶�������P��PD��AC�ڵ�D����PDΪ�����Ҳ���������PDEF������Q��QG��AB��������BC��CA�ڵ�G���C���غϣ���QGΪ��������ֱ�ǡ�QGH���ҵ�GΪֱ�Ƕ��㣬��C��Hʼ����QG��ͬ�࣬��������PDEF���QGH�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����0��t��4����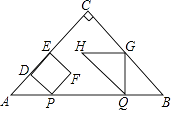
��1������F�ڱ�QH��ʱ����t��ֵ��
��2����������PDEF���QGH�ص�����ͼ�����ı���ʱ����S��t֮��ĺ�����ϵʽ��
��3����FH���ڵ�ֱ��ƽ�л�ֱ��ABʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+b�ֱ���x�ᡢy�ύ��A��B���㣬����B��������y=�� ![]() ��x��2��2+m�Ķ���P������ֱ���ϣ���ABΪ�����·���������ABCD��
��x��2��2+m�Ķ���P������ֱ���ϣ���ABΪ�����·���������ABCD��
��1����m=2ʱ��k= �� b=����m=��1ʱ��k= �� b=��
��2�����ݣ�1���еĽ�����ú�m�Ĵ���ʽ�ֱ��ʾk��b����֤����Ľ��ۣ�
��3����������ABCD�Ķ���C���������ߵĶԳ�����ʱ�����Ӧ�������ߵĺ�����ϵʽ��
��4����������ABCD�Ķ���D������������ʱ��ֱ��д����Ӧ��ֱ��y=kx+b�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
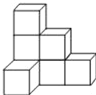
����Ŀ���������ϣ���7����ȫ��ͬ��С������ѳɵ�һ��������A����ͼ��ʾ.
(1) �뻭�����������A������ͼ.
(2) �����˼�����ı������Ϻ���(���������ϵ�һ�治��)�������������Ǻ�ɫ��С��������______��.
(3) �����������ͷ����һЩ��ͬ��С������������ڸü������ϣ�Ҫ���ָ���ͼ������ͼ���䣬������������_______��С������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OEƽ�֡�AOC��OFƽ�֡�BOC���ҡ�BOC=60��������AOC+��EOF=156�������EOF�Ķ����ǣ�������

A. 88�� B. 30�� C. 32�� D. 48��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʢʢͬѧ��ij��У����ʱ�������˶������������еIJ�����Ϣ�����±�����
Ժϵ�������ɼ����� | |||
�������� | ʤ�� | ���� | ���� |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
ʢʢͬѧ���ѧϰ��֪ʶ������������⣬�����æ����������⣺
��1���ӱ��п��Կ�������һ����______��,ʤһ����_______����
��2��ij���ڱ���22����ǰ���£�ʤ���ܻ����ܵ����为���ܻ��ֵ�2������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ճ������г��������⣬��ͼ��������BC���ݶ���һ�����AB���ӵ�����D�㴦�۲���˶���A������Ϊ50�㣬�۲���˵ײ�B�������Ϊ45�㣬�����õIJο����ݣ�sin50���0.8��tan50���1.2��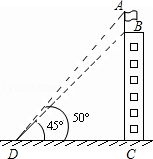
��1������֪CD=20�ף�������BC�ĸ߶ȣ�
��2������֪��˵ĸ߶�AB=5�ף�������BC�ĸ߶ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com