
����Ŀ����Rt��ABC�У�BC��AC����ACB��90�㣬DΪ����AB��һ�㣬����CD������C���߶�CD�Ĵ���l����ֱ��l�ϣ��ֱ��ڵ�C�������ȡ���߶�CD��ȵ��߶�CE��CF������AE��BF.
(1)����D���߶�AB��ʱ(��D�����A��B�غ�)����ͼ23(a)��
�����㽫ͼ�β���������
���߶�BF��AD����ֱ�ߵ�λ�ù�ϵΪ________���߶�BF��AD��������ϵΪ________��
(2)����D���߶�AB���ӳ�����ʱ����ͼ23(b)��
��(1)�Т��ʵĽ����Ƿ���Ȼ��������������������֤�����������������˵�����ɣ�

���𰸡�(1)�ټ�����;�ڴ�ֱ�����;(2)����,���ɼ�����.
��������
(1)����ͼ��ʾ��

�ڸ���CD��EF,�ɵá�DCF��90��.���ڡ�ACB��90��,�ɵá�ACB����DCF,��ACD����BCF.
����AC��BC,CD��CF,���ж���ACD�ա�BCF,����ȫ�������ε����ʿɵ�AD��BF,��BAC����FBC,�̶��ɵá�ABF����ABC����FBC����ABC����BAC��90��,��BF��AD.
(2)����CD��EF,�ɵá�DCF��90��,���ڡ�ACB��90��,��֤��DCF����ACB,
���ԡ�DCF����BCD����ACB����BCD,�̶��ɵá�BCF����ACD,����AC��BC,CD��CF,
���ж���ACD�ա�BCF,����ȫ�������ε����ʿɵ�AD��BF,��BAC����FBC,���ԡ�ABF����ABC����FBC����ABC����BAC��90��,��BF��AD.
��:(1)����ͼ��ʾ��

�ڡ�CD��EF,
���DCF��90��.
�ߡ�ACB��90��,
���ACB����DCF,
���ACD����BCF.
�֡�AC��BC,CD��CF,
���ACD�ա�BCF,
��AD��BF,��BAC����FBC,
���ABF����ABC����FBC����ABC����BAC��90��,��BF��AD.
�ʴ�Ϊ:��ֱ,���.
(2)������
֤��:��CD��EF,
���DCF��90��,
�ߡ�ACB��90��,
���DCF����ACB,
���DCF����BCD����ACB����BCD,
���BCF����ACD,
�֡�AC��BC,CD��CF,
���ACD�ա�BCF,
��AD��BF,��BAC����FBC,
���ABF����ABC����FBC����ABC����BAC��90��,��BF��AD.


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90��
��1���ó߹���AB�Ĵ�ֱƽ����MN��BC�ڵ�P����д������������ͼ�ۼ�����
��2������AP�����APƽ�֡�CAB�����B�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
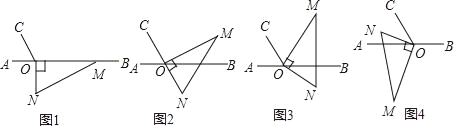
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��AOC=60������һ��ֱ�����dzߵ�ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
��1����ͼ1�е����dz��Ƶ�O��ʱ����ת��ͼ2��ʹ��N��OC�ķ����ӳ����ϣ���ֱ��д��ͼ����MOB�Ķ�����
��2����ͼ1�е����dz��Ƶ�O��ʱ����ת��ͼ3��ʹһ��OM����BOC���ڲ�����ǡ��ƽ����BOC������CON�Ķ�����
��3����ͼ1�е����dz��Ƶ�O˳ʱ����ת��ͼ4��ʹON����AOC���ڲ�����̽����AOM����NOC֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Խ��Խ�ܵ����ǵ�ϲ����˳�糵�о�Ӫ��A�ͳ�2016��4�·������ܶ�Ϊ3.2��Ԫ�����꾭������������A�ͳ�ÿ�����۱�ȥ������400Ԫ��������4�·���ȥ��4�·�������A�ͳ�������ͬ�������4�·�A�ͳ������ܶ��ȥ��4�·������ܶ�����25%�� A��B�����ͺų��Ľ��������ۼ۸������
A�ͳ� | B�ͳ� | |
�����۸�Ԫ/���� | 1100 | 1400 |
���ۼ۸�Ԫ/���� | ��������ۼ۸� | 2400 |
��1�������4�·�A�ͳ�ÿ�����ۼ۶���Ԫ�����з��̵ķ�����𣩣�
��2���ó��мƻ�5�·��½�һ��A�ͳ���B�ͳ���50������B�ͳ��Ľ�������������A�ͳ�������������Ӧ��ν�������ʹ������������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ֵ��֪ʶ�ش��������⣺
�����ϱ�ʾ4��1������֮��ľ�����3����|4-1|=3����ʾ-3��2����֮��ľ�����5����|-3-2|=5����ʾ-4��-7����֮��ľ�����3����|-4-��-7��|=3��
һ��أ������ϱ�ʾ��m����n������֮��ľ��빫ʽΪ|m-n|��
(1)�����ϱ�ʾ��-5�ĵ����ʾ-2�ĵ�֮��ľ���Ϊ______��
(2)�����ϱ�ʾ��a�ĵ����ʾ-4�ĵ�֮��ľ����ʾΪ______����������aλ��-4��2֮�䣬��|a+4|+|a-2|��ֵ��
(3)�����ʾ��a��3������֮��ľ�����7����ɼ�Ϊ��|a-3|=7����a��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������A��B��������ʾ�����ֱ�Ϊ��2��8.
(1)���߶�AB�ij���
(2)��PΪ����BA�ϵ�һ��(��P����A��B�����غϣ�MΪPA���е㣬NΪPB���е㣬����P������BA���˶�ʱ��MN�ij����Ƿ����ı䣿�����䣬���㻭��ͼ�Σ�������߶�MN�ij������ı䣬��˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������A��B�����Ӧ����Ϊ0��10��PΪ������һ��
��1����PΪAB�߶ε��е㣬��P��Ӧ����Ϊ�� ����
��2���������е�P��ʹP��A��B�ľ���֮��Ϊ20����P��Ӧ����Ϊ�� ����
��3������P���ʾ6����M��ÿ����5����λ���ٶȴ�A�������˶�����N��ÿ����1����λ���ٶȴ�B�������˶���t�����PM=PN����ʱ��t��ֵ����ͼд���̣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+5��x�ύ��A��1��0����B��5��0�����㣬��D���������Ϻ�����Ϊ6�ĵ㣮��P�������������ϣ��Ҳ���A��D�����غϣ�����P��y���ƽ����������AD���ڵ�Q������Q��QF��ֱ��y�ᣬ��F�ڵ�Q���Ҳ࣬��QF=2����QF��QPΪ�ڱ�������QPEF�������QPEF���ܳ�Ϊd����P�ĺ�����Ϊm��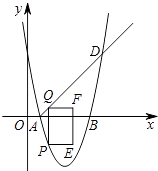
��1������������������Ӧ�ĺ�������ʽ��
��2�������������ߵĶԳ��Ὣ����QPEF�������Ϊ1��2������ʱm��ֵ��
��3����d��m֮��ĺ�����ϵʽ��d��m���������Сʱd��ȡֵ��Χ��
��4��������QPEF�ĶԽ����ഹֱʱ��ֱ��д����Գ����ĵĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�ֱ��AB��x�Ḻ���ύ�ڵ�A��a��0������ y�������ύ�ڵ�B��0��b������![]() +|b��4|=0��
+|b��4|=0��

��1�����AOB�������
��2����ͼ2����PΪֱ��AB��һ���㣬����OP����2S��AOP��S��BOP��3S��AOP����P�������xP��ȡֵ��Χ��
��3����ͼ3����C�ڵ�������ֱ��AB�ϣ�����OC��OE��OC��O������CE��y ���ڵ�D������AD��OE���ӳ�����F�����OAD����ADC����CEF����AOC֮���Ƿ���ij��ȷ����������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com