
【题目】已知数轴上A、B两点对应的数为0、10,P为数轴上一点
(1)点P为AB线段的中点,点P对应的数为 .
(2)数轴上有点P,使P到A,B的距离之和为20,点P对应的数为 .
(3)若点P点表示6,点M以每秒钟5个单位的速度从A点向右运动,点N以每秒钟1个单位的速度从B点向右运动,t秒后有PM=PN,求时间t的值(画图写过程).
【答案】(1)5;(2) ﹣5 或 15 ;(3) ![]() 或 2.5.
或 2.5.
【解析】
(1)根据中点坐标公式即可求解;(2)分①P 在 A 的左边,②P 在 B 的右边两种情况讨论即可求解;分①M 在 P 的左边,②M 在 P 的右边两种情况讨论即可求
(1)(0+10)÷2=5.故点 P 对应的数为:5 故答案为:5.
(2)①分 P 在 A 的左边,点 P 对应的数是﹣5,②P 在 B 的右边,点 P 对应的数是 15,故点 P 对应的数为﹣5 或 15.
故答案为:﹣5 或 15.
③①M 在 P 的左边,依题意有: 6﹣5t=t+(10﹣6),解得 t=![]() ,
,
②M 在 P 的右边,依题意有:5t﹣6=t+(10﹣6),解得 t=2.5.
故 t 的值为![]() 或 2.5.
或 2.5.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( ) 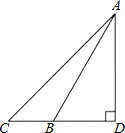
A.2 ![]() m
m
B.2 ![]() m
m
C.(2 ![]() ﹣2)m
﹣2)m
D.(2 ![]() ﹣2)m
﹣2)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足OA=3,BC=1,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒1.5个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 ![]() cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 .
cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.. 计算题:
(1)8﹣(﹣10)﹣|﹣2|
(2)2 ![]() ﹣3
﹣3![]() +(﹣3
+(﹣3![]() )﹣(+5
)﹣(+5![]() )
)
(3)﹣24×(﹣ ![]() +
+![]() ﹣
﹣![]() )
)
(4)﹣49 ![]() ×10(简便运算)
×10(简便运算)
(5)﹣ ![]() ÷(
÷(![]() ﹣
﹣![]() +
+![]() )
)
(6)3×(﹣38 ![]() )﹣4×(﹣38
)﹣4×(﹣38 ![]() )﹣38
)﹣38![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y= ![]() (k>0)图象与AC边交于点E.
(k>0)图象与AC边交于点E. 
(1)请用k表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB∥CD,点P为定点,E、F分别是AB、CD上的动点.
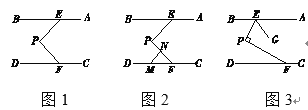
(1)求证:∠P=∠BEP+∠PFD;
(2)若点M为CD上一点,如图2,∠FMN=∠BEP,且MN交PF于N.试说明∠EPF与∠PNM的数量关系,并证明你的结论;
(3)移动E、F使得∠EPF=90°,如图3,作∠PEG=∠BEP,求∠AEG与∠PFD度数的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(2x+y﹣3,x﹣2y),它关于x轴的对称点A1的坐标为(x+3,y﹣4),关于y轴的对称点为A2.
(1)求A1、A2的坐标;
(2)证明:O为线段A1A2的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
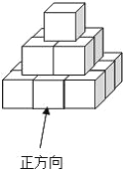
【题目】把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com