
【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足OA=3,BC=1,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒1.5个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时,求OP的长.

【答案】(1)-3,6;(2)点Q的运动速度每秒1个单位长度;(3)OP的长为0.6或6.6.
【解析】
(1)由点C表示7,可得OC=7,由OA=3,BC=1,得A、B两点表示的数,可得a、b的值;
(2)先计算P运动时间,根据点Q运动的位置恰好是线段AB靠近点B的三等分点,可知:BQ=![]() AB,可得点Q的路程,根据时间可得结论;
AB,可得点Q的路程,根据时间可得结论;
(3)设t秒时,PQ=6,分两种情况:①如图1,当Q在P的右侧时,②如图2,当Q在P的左侧时;根据PQ=6分别列式可得t的值,再计算OP的长.
(1)∵OA=3,
∴点A表示的数为﹣3,即a=﹣3,
∵C表示的数为7,
∴OC=7,
∵BC=1,
∴OB=6,
∴点B表示的数为6,即b=6;
(2)当P为OB的中点时,
AP=AO+OP=3+![]() OB=3+3=6,
OB=3+3=6,
t=![]() =4(s),
=4(s),
由题意得:BQ=![]() AB=
AB=![]() ×(3+6)=3,
×(3+6)=3,
∴CQ=BQ+BC=1+3=4,
∴VQ=![]() =1,
=1,
答:点Q的运动速度每秒1个单位长度;
(3)设t秒时,PQ=6,
分两种情况:
①如图1,当Q在P的右侧时,

AP+PQ+CQ=3+7,
1.5t+6+t=3+7,
t=1.6,
AP=1.5t=2.4,
∴OP=3﹣2.4=0.6,
②如图2,当Q在P的左侧时,

AP+CQ=AC+PQ=10+6,
1.5t+t=16,
t=6.4,
AP=1.5t=1.5×6.4=9.6,
∴OP=9.6﹣3=6.6,
综上所述,OP的长为0.6或6.6.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )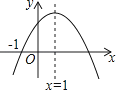
A.a>0
B.c<0
C.3是方程ax2+bx+c=0的一个根
D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算
①(1﹣![]() )×(1+
)×(1+![]() )= ,1﹣(
)= ,1﹣(![]() )2= ; 有(1﹣
)2= ; 有(1﹣![]() )×(1+
)×(1+![]() ) 1﹣(
) 1﹣(![]() )2 (用“=”“<”“>”填空).
)2 (用“=”“<”“>”填空).
②(1﹣![]() )×(1+
)×(1+![]() )= ,1﹣(
)= ,1﹣(![]() )2= ; 有(1﹣
)2= ; 有(1﹣![]() )×(1+
)×(1+![]() ) 1﹣(
) 1﹣(![]() )2 (用“=”“<”“>”填空).
)2 (用“=”“<”“>”填空).
③猜测(1﹣![]() )(1+
)(1+![]() )与1﹣(
)与1﹣(![]() )2 有关系:(1﹣
)2 有关系:(1﹣![]() )(1+
)(1+![]() ) 1﹣(
) 1﹣(![]() )2.(用“=”“<”“>”填空)
)2.(用“=”“<”“>”填空)
(2)计算:[1﹣(![]() )2]×[1﹣(
)2]×[1﹣(![]() )2]×[1﹣(
)2]×[1﹣(![]() )2]×…×[1﹣(
)2]×…×[1﹣(![]() )2]
)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价(元/kg) | 3.6 | 5.4 | 8 | 4.8 |
零售价(元/吨) | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300 kg,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?
(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后赚钱数1050元,则该经营户批发西红柿多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=k1x+b与x轴,y轴相交于P,Q两点,则y= ![]() 的图象相交于A(﹣2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+ ![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b> ![]() 的解集在x<﹣2或0<x<1,其中正确的结论是( )
的解集在x<﹣2或0<x<1,其中正确的结论是( ) 
A.②③④
B.①②③④
C.③④
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A、B两点对应的数为0、10,P为数轴上一点
(1)点P为AB线段的中点,点P对应的数为 .
(2)数轴上有点P,使P到A,B的距离之和为20,点P对应的数为 .
(3)若点P点表示6,点M以每秒钟5个单位的速度从A点向右运动,点N以每秒钟1个单位的速度从B点向右运动,t秒后有PM=PN,求时间t的值(画图写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE交直线a于点E,且∠ADE=60°.
(1)若D在BC上(如图1)求证CD+CE=CA;

(2)若D在CB延长线上,CD、CE、CA存在怎样数量关系,给出你的结论并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com