
【题目】(1)计算
①(1﹣![]() )×(1+
)×(1+![]() )= ,1﹣(
)= ,1﹣(![]() )2= ; 有(1﹣
)2= ; 有(1﹣![]() )×(1+
)×(1+![]() ) 1﹣(
) 1﹣(![]() )2 (用“=”“<”“>”填空).
)2 (用“=”“<”“>”填空).
②(1﹣![]() )×(1+
)×(1+![]() )= ,1﹣(
)= ,1﹣(![]() )2= ; 有(1﹣
)2= ; 有(1﹣![]() )×(1+
)×(1+![]() ) 1﹣(
) 1﹣(![]() )2 (用“=”“<”“>”填空).
)2 (用“=”“<”“>”填空).
③猜测(1﹣![]() )(1+
)(1+![]() )与1﹣(
)与1﹣(![]() )2 有关系:(1﹣
)2 有关系:(1﹣![]() )(1+
)(1+![]() ) 1﹣(
) 1﹣(![]() )2.(用“=”“<”“>”填空)
)2.(用“=”“<”“>”填空)
(2)计算:[1﹣(![]() )2]×[1﹣(
)2]×[1﹣(![]() )2]×[1﹣(
)2]×[1﹣(![]() )2]×…×[1﹣(
)2]×…×[1﹣(![]() )2]
)2]
【答案】(1)①![]() 、
、![]() 、=;②
、=;②![]() 、
、![]() 、=;③=;(2)
、=;③=;(2)![]()
【解析】
(1)①根据有理数的运算法则依次计算后即可解答;②根据有理数的运算法则依次计算后即可解答;③类比①②的计算结果即可解答;(2)利用(1)获得的方法,把把中括号内的每一个式子分解后再计算即可求解.
解:(1)①(1﹣![]() )×(1+
)×(1+![]() )=
)=![]() ,1﹣(
,1﹣(![]() )2=
)2=![]() ;有(1﹣
;有(1﹣![]() )×(1+
)×(1+![]() )=1﹣(
)=1﹣(![]() )2.
)2.
②(1﹣![]() )×(1+
)×(1+![]() )=
)=![]() ,1﹣(
,1﹣(![]() )2=
)2=![]() ;有(1﹣
;有(1﹣![]() )×(1+
)×(1+![]() )=1﹣(
)=1﹣(![]() )2
)2
③猜测(1﹣![]() )(1+
)(1+![]() )与1﹣(
)与1﹣(![]() )2 有关系:(1﹣
)2 有关系:(1﹣![]() )(1+
)(1+![]() )=1﹣(
)=1﹣(![]() )2.
)2.
故答案为:①![]() 、
、![]() 、=;②
、=;②![]() 、
、![]() 、=;③=
、=;③=
(2)原式=(1﹣![]() )×(1+
)×(1+![]() )×(1﹣
)×(1﹣![]() )×(1+
)×(1+![]() )×(1﹣
)×(1﹣![]() )×(1+
)×(1+![]() )…(1﹣
)…(1﹣![]() )×(1+
)×(1+![]() )
)
=![]()
=![]() ×
×![]()
=![]() .
.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF//BC交AC于M,若CM=5,则CE2+CF2等于( )

A. 100 B. 75 C. 120 D. 125
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( ) 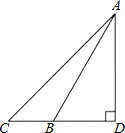
A.2 ![]() m
m
B.2 ![]() m
m
C.(2 ![]() ﹣2)m
﹣2)m
D.(2 ![]() ﹣2)m
﹣2)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:(a×b)2=a2×b2、(a×b)3=a3×b3、(a×b)4=a4×b4,
(1)用具体数值验证上述等式是否成立(写出其中一个验证过程)
(2)通过上述验证,猜一猜:(a×b)100= ,归纳得出:(a×b)n= ;
(3)请应用上述性质计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2 , 当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足OA=3,BC=1,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒1.5个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB∥CD,点P为定点,E、F分别是AB、CD上的动点.
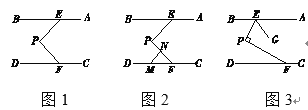
(1)求证:∠P=∠BEP+∠PFD;
(2)若点M为CD上一点,如图2,∠FMN=∠BEP,且MN交PF于N.试说明∠EPF与∠PNM的数量关系,并证明你的结论;
(3)移动E、F使得∠EPF=90°,如图3,作∠PEG=∠BEP,求∠AEG与∠PFD度数的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com