
【题目】如图1,AB∥CD,点P为定点,E、F分别是AB、CD上的动点.
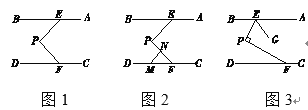
(1)求证:∠P=∠BEP+∠PFD;
(2)若点M为CD上一点,如图2,∠FMN=∠BEP,且MN交PF于N.试说明∠EPF与∠PNM的数量关系,并证明你的结论;
(3)移动E、F使得∠EPF=90°,如图3,作∠PEG=∠BEP,求∠AEG与∠PFD度数的比值.
【答案】(1)详见解析;(2)∠EPF=∠PNM.(3)2∶1.
【解析】
(1)如图1,过点P作PG∥AB,根据平行线的性质进行证明;
(2)利用(1)中的结果和三角形外角的性质可以推知∠EPF=∠PNM;
(3)利用(1)中的结论得到∠1+∠2=90°,结合已知条件∠PEG=∠BEP,即∠1=∠3得到∠4=180°-2∠1,易求∠AEG与∠PFD度数的数量关系.
解:(1)证明:如答图(1),过点P作PG∥AB,则∠1=∠BEP.
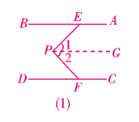
又∵AB∥CD,∴PG∥CD,∴∠2=∠PFD,
∴∠EPF=∠1+∠2=∠BEP+∠PFD,即∠EPF=∠BEP+∠PFD.
(2)∠EPF=∠PNM.证明如下:
由(1)知,∠EPF=∠BEP+∠PFD.
如答图(2),
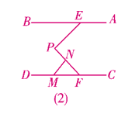
∵∠FMN=∠BEP,
∴∠EPF=∠FMN+∠PFD.
又∵∠PNM=∠FMN+∠PFD,
∴∠EPF=∠PNM.
(3)如答图(3),
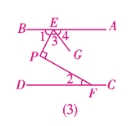
∵由(1)知∠1+∠2=90°.
∴∠2=90°-∠1.
又∵∠1=∠3,
∴∠4=180°-2∠1=2∠2,
∴∠4∶∠2=2∶1.
即∠AEG与∠PFD度数的比值为2∶1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)计算
①(1﹣![]() )×(1+
)×(1+![]() )= ,1﹣(
)= ,1﹣(![]() )2= ; 有(1﹣
)2= ; 有(1﹣![]() )×(1+
)×(1+![]() ) 1﹣(
) 1﹣(![]() )2 (用“=”“<”“>”填空).
)2 (用“=”“<”“>”填空).
②(1﹣![]() )×(1+
)×(1+![]() )= ,1﹣(
)= ,1﹣(![]() )2= ; 有(1﹣
)2= ; 有(1﹣![]() )×(1+
)×(1+![]() ) 1﹣(
) 1﹣(![]() )2 (用“=”“<”“>”填空).
)2 (用“=”“<”“>”填空).
③猜测(1﹣![]() )(1+
)(1+![]() )与1﹣(
)与1﹣(![]() )2 有关系:(1﹣
)2 有关系:(1﹣![]() )(1+
)(1+![]() ) 1﹣(
) 1﹣(![]() )2.(用“=”“<”“>”填空)
)2.(用“=”“<”“>”填空)
(2)计算:[1﹣(![]() )2]×[1﹣(
)2]×[1﹣(![]() )2]×[1﹣(
)2]×[1﹣(![]() )2]×…×[1﹣(
)2]×…×[1﹣(![]() )2]
)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=k1x+b与x轴,y轴相交于P,Q两点,则y= ![]() 的图象相交于A(﹣2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+ ![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b> ![]() 的解集在x<﹣2或0<x<1,其中正确的结论是( )
的解集在x<﹣2或0<x<1,其中正确的结论是( ) 
A.②③④
B.①②③④
C.③④
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A、B两点对应的数为0、10,P为数轴上一点
(1)点P为AB线段的中点,点P对应的数为 .
(2)数轴上有点P,使P到A,B的距离之和为20,点P对应的数为 .
(3)若点P点表示6,点M以每秒钟5个单位的速度从A点向右运动,点N以每秒钟1个单位的速度从B点向右运动,t秒后有PM=PN,求时间t的值(画图写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A、M两点之间和B、O两点之间上运动时(点P与点A、B、O三点不重合),请你分别直接写出∠CPD、∠α、∠β之间的数量关系.
 ,图1)
,图1)  ,图2)
,图2)
 ,图3)
,图3)  ,备用图)
,备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=110°,则∠1+∠2的度数为( )

A. 80°; B. 90°; C. 100°; D. 110°;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ![]() ,tan48°≈
,tan48°≈ ![]() ,sin64°≈
,sin64°≈ ![]() ,tan64°≈2)
,tan64°≈2)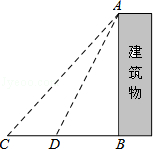
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE交直线a于点E,且∠ADE=60°.
(1)若D在BC上(如图1)求证CD+CE=CA;

(2)若D在CB延长线上,CD、CE、CA存在怎样数量关系,给出你的结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( )

A. ∠BAC=70° B. ∠DOC=90° C. ∠BDC=35° D. ∠DAC=55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com